Contoh Soal Segitiga Siku-Siku, Lengkap dengan Pembahasannya
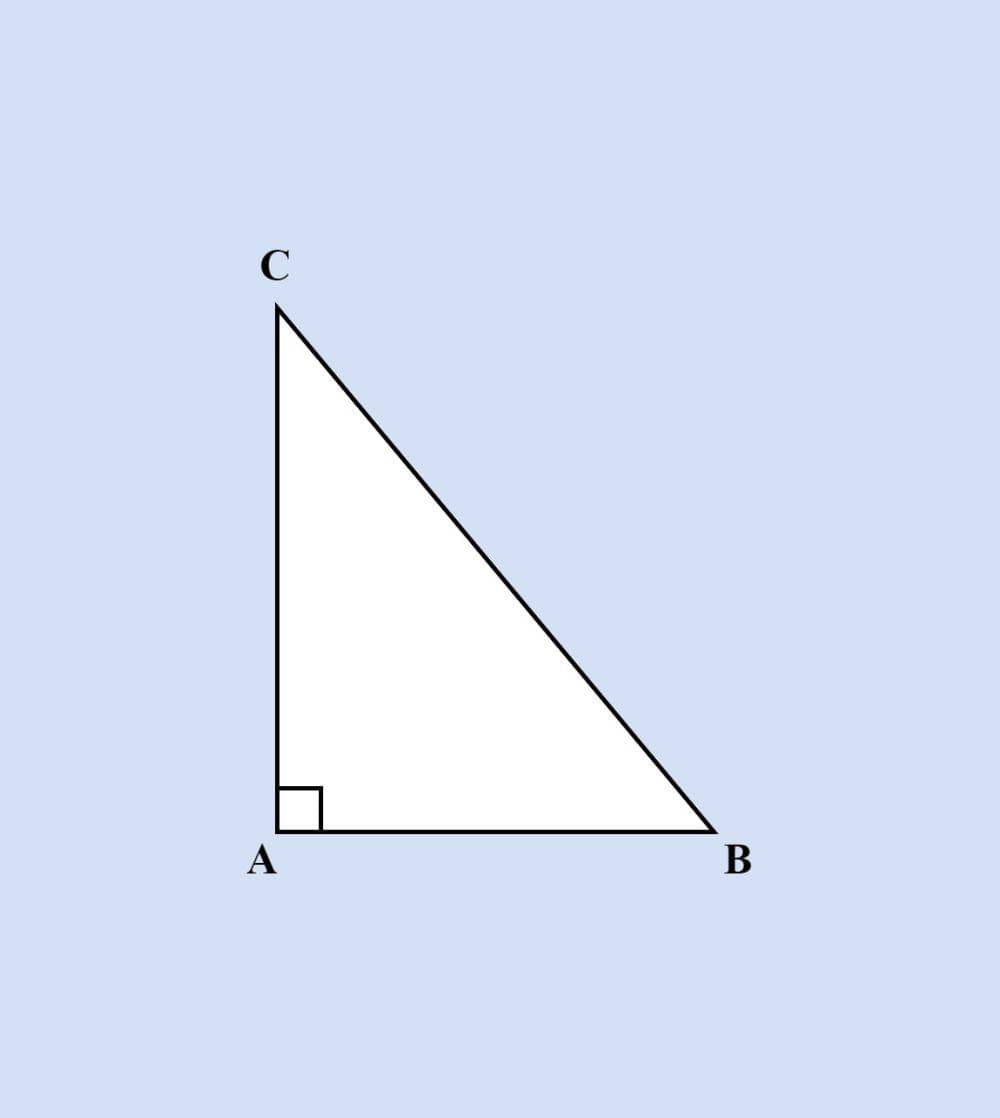
Segitiga siku-siku merupakan salah satu jenis segitiga yang menarik untuk dibahas. Sebagaimana segitiga pada umumnya, segitiga siku-siku juga terdiri dari tiga garis yang membentuk tiga sisi dan tiga sudut. Yang membedakan segitiga siku-siku adalah keberadaan satu sudut yang berbentuk siku-siku yang memiliki besar sudut 90 derajat.
Berikut adalah rumus luas, keliling, dan teorema Pythagoras pada segitiga siku-siku, beserta penerapan dan pembahasannya dalam soal.
1. Rumus luas dan keliling segitiga siku-siku
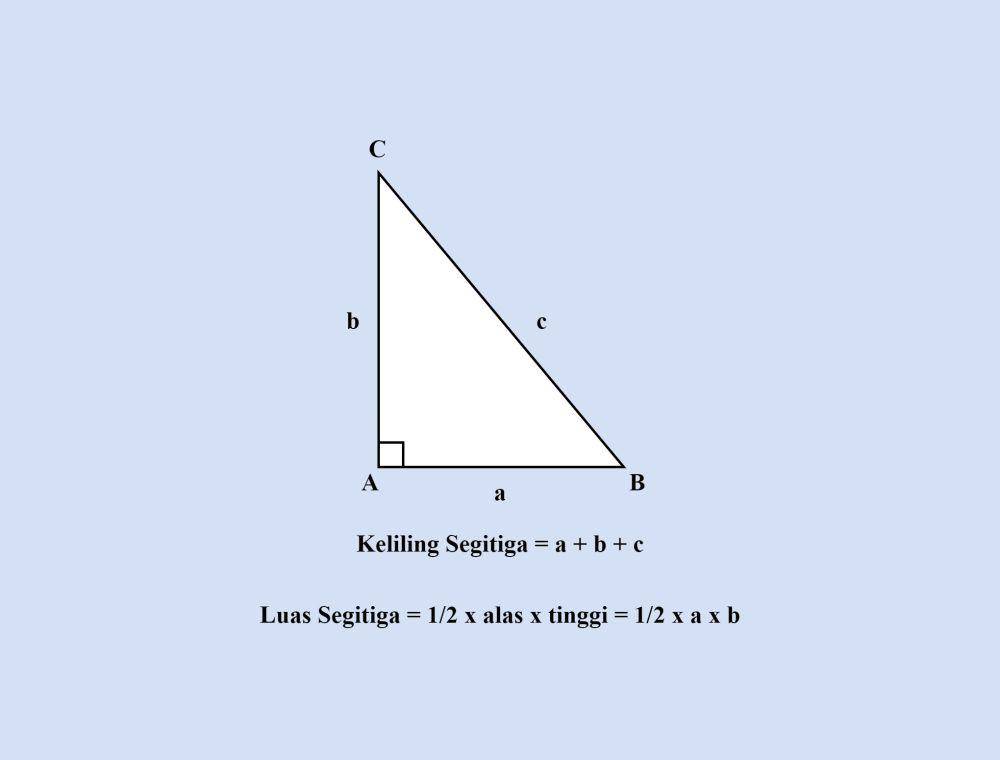
Luas segitiga siku-siku dapat dihitung dengan rumus ½ x alas x tinggi. Untuk menghitung keliling segitiga siku-siku, kita dapat menjumlahkan panjang semua sisinya. Jika panjang sisi segitiga siku-siku disimbolkan sebagai a, b, dan c, maka rumus menghitung kelilingnya adalah a + b + c.
2. Teorema Pythagoras
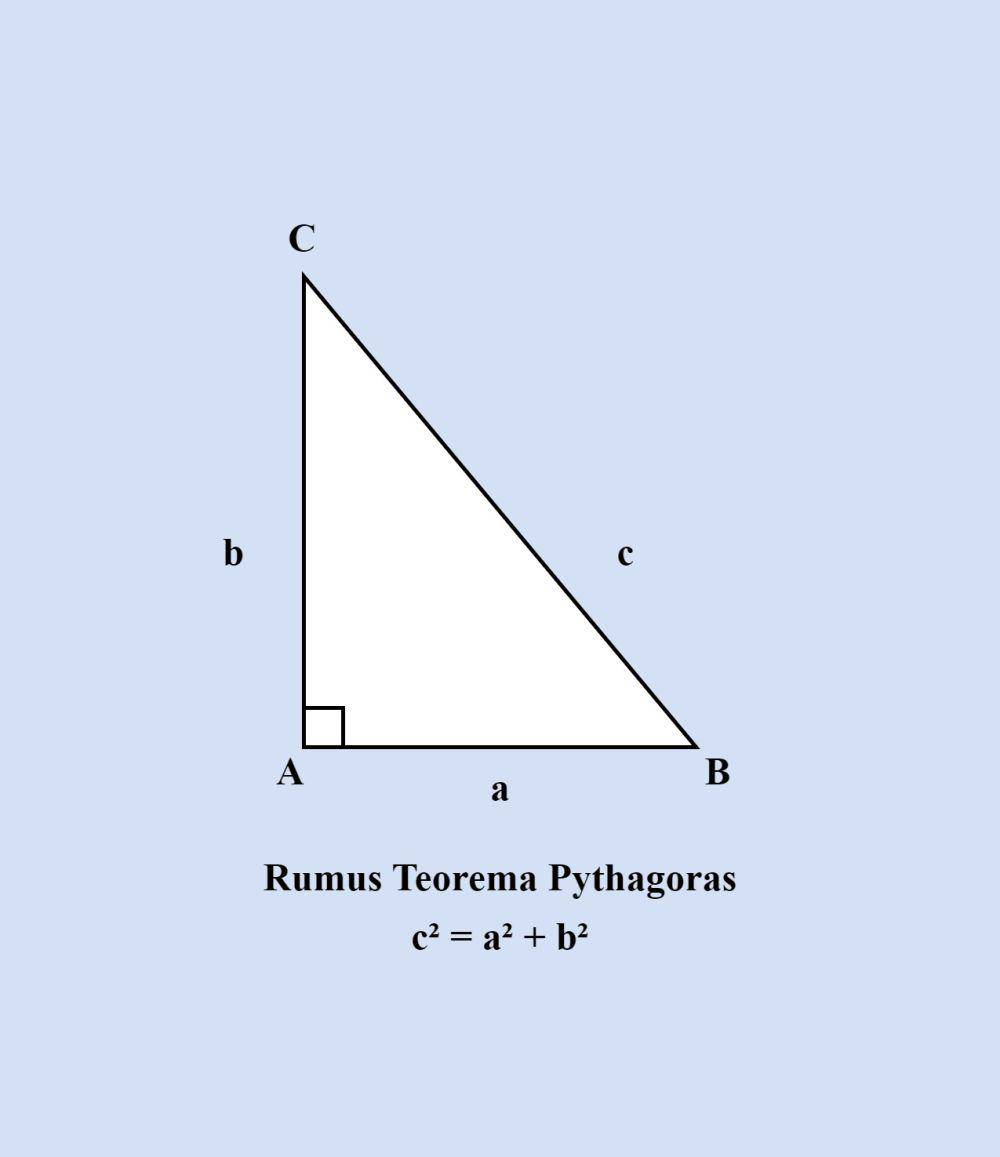
Dalam segitiga siku-siku, sisi yang berhadapan dengan sudut siku-siku disebut hipotenusa, yang merupakan sisi miring segitiga. Sementara itu, sisi yang membentuk sudut siku-siku disebut kaki-kaki segitiga, yang merupakan alas dan tinggi segitiga. Panjang kedua kaki segitiga ini dapat dihitung menggunakan Pythagoras, yaitu teorema yang menghubungkan panjang sisi-sisi segitiga siku-siku. Panjang hipotenusa (c) dapat ditemukan dengan menghitung akar kuadrat dari jumlah kuadrat panjang kedua kaki segitiga (a dan b), atau c² = a² + b².
3. Contoh soal menghitung luas segitiga siku-siku dan pembahasannya
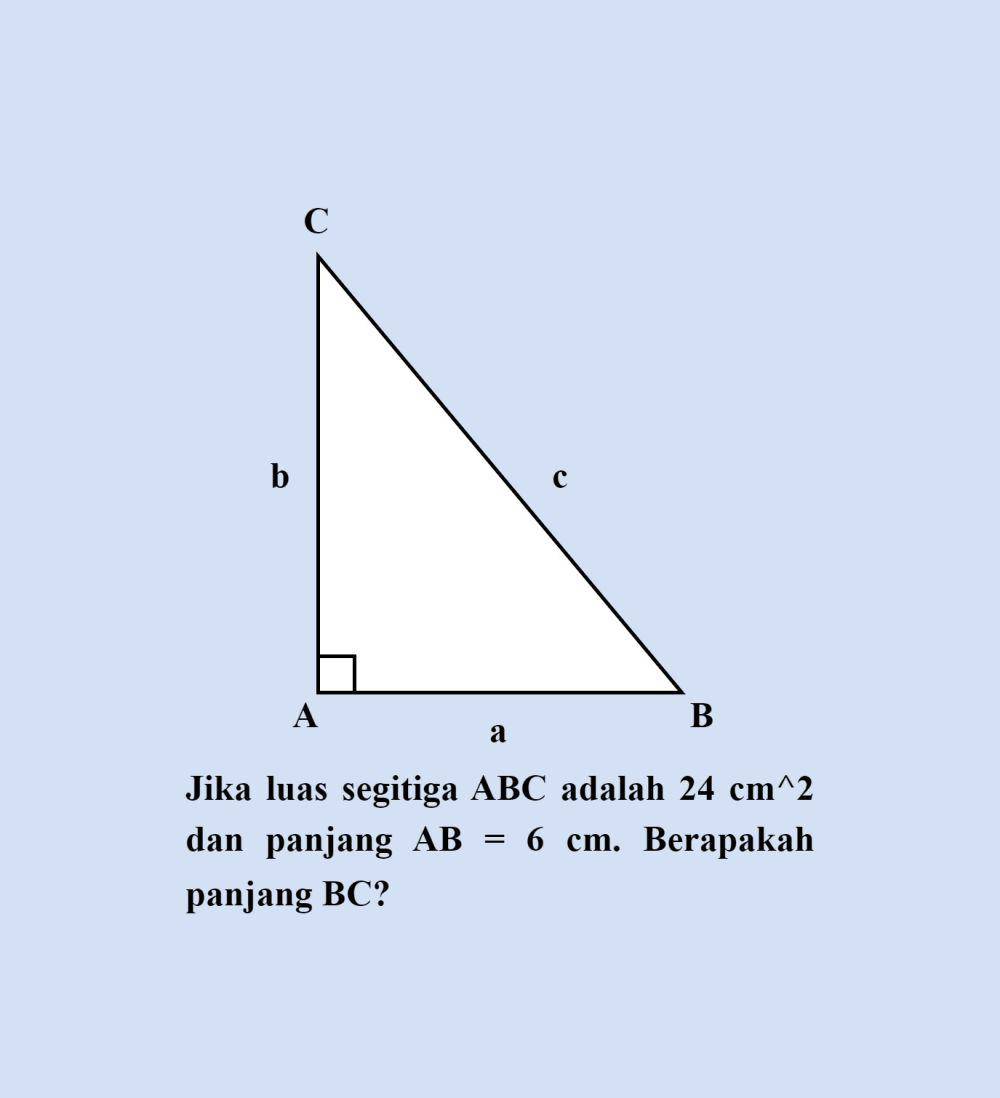
Pembahasan:
Diketahui:
Luas segitiga ABC = 24 cm²
AB = 6 cm
Ditanya:
BC = ?
Jawaban:
Langkah pertama yang harus dilakukan adalah mencari tinggi segitiga (AC) dengan memanfaatkan nilai luas dan panjang alas yang sudah diketahui.
Luas = ½ x alas x tinggi
24 = ½ x 6 x AC
24 x 2 = 6 x AC
48 = 6AC
AC = 48 : 6
AC = 8
Jadi tinggi segitiga ABC adalah 8 cm
Langkah selanjutnya adalah mencari panjang BC dengan menggunakan rumus teorema Pythagoras. BC adalah hipotenusa (c), AB (a) adalah alas dan AC (b) adalah tinggi segitiga siku-siku ABC.
Maka cara mencari panjang BC adalah sebagai berikut.
c² = a² + b²
BC² = AB² + AC²
BC² = 6² + 8²
BC² = 36 + 64
BC² = 100
BC = 10
Jadi panjang BC adalah 10 cm.
4. Contoh soal menghitung luas segitiga siku-siku dan pembahasannya
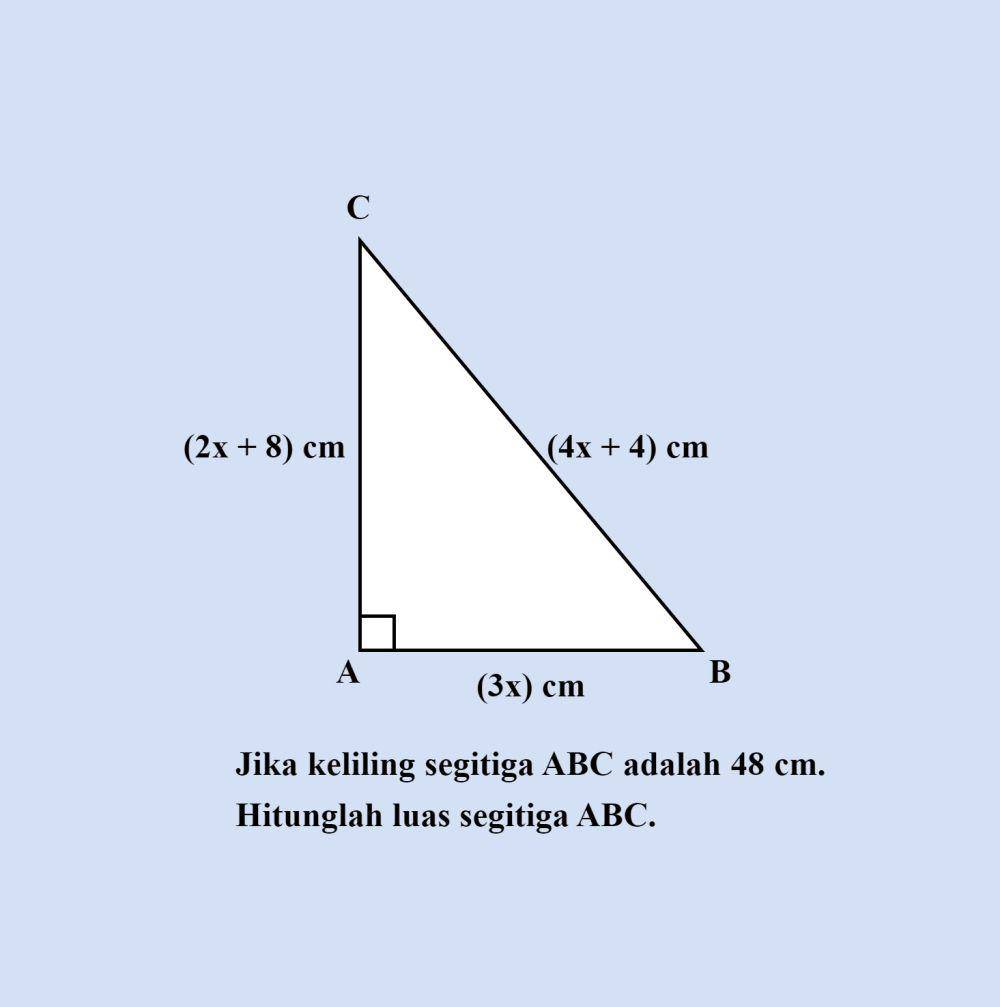
Pembahasan:
Diketahui:
Keliling segitiga ABC = 48 cm
Panjang alas segitiga ABC = (3x) cm
Tinggi segitiga ABC = (2x+8) cm
Panjang sisi miring segitiga ABC = (4x+4) cm
Ditanya:
Luas segitiga ABC = ?
Jawaban:
Langkah pertama yang harus dilakukan adalah mencari nilai x untuk mendapatkan panjang alas dan tinggi segitiga ABC. Nilai x dapat dicari dengan memanfaatkan nilai keliling yang sudah diketahui.
Misalkan panjang alas segitiga disimbolkan sebagai a, tinggi segitiga sebagai b, dan panjang sisi miring segitiga sebagai c.
Keliling = 48
a + b + c = 48
(3x) + (2x+8) + (4x+4) = 48
3x + 2x + 4x + 8 + 4 = 48
9x + 12 = 48
9x = 48 - 12
9x = 36
x = 36 : 9
x = 4
Langkah kedua adalah menghitung panjang setiap sisi pada segitiga ABC dengan mensubstitusi nilai x.
karena x = 4, maka:
Panjang alas segitiga ABC = (3x) cm = 3x4 = 12 cm
Tinggi segitiga ABC = (2x+8) cm = (2x4)+8 = 16 cm
Panjang sisi miring segitiga ABC = (4x+4) cm = (4x4) + 4 = 20 cm
Langkah ketiga baru menghitung luas segitiga ABC.
Luas = ½ x alas x tinggi
Luas = ½ x 12 x 16
Luas = 6 x 16
Luas = 96 cm²
Jadi luas segitiga ABC adalah 96 cm².
5. Contoh soal menghitung luas segitiga siku-siku dan pembahasannya
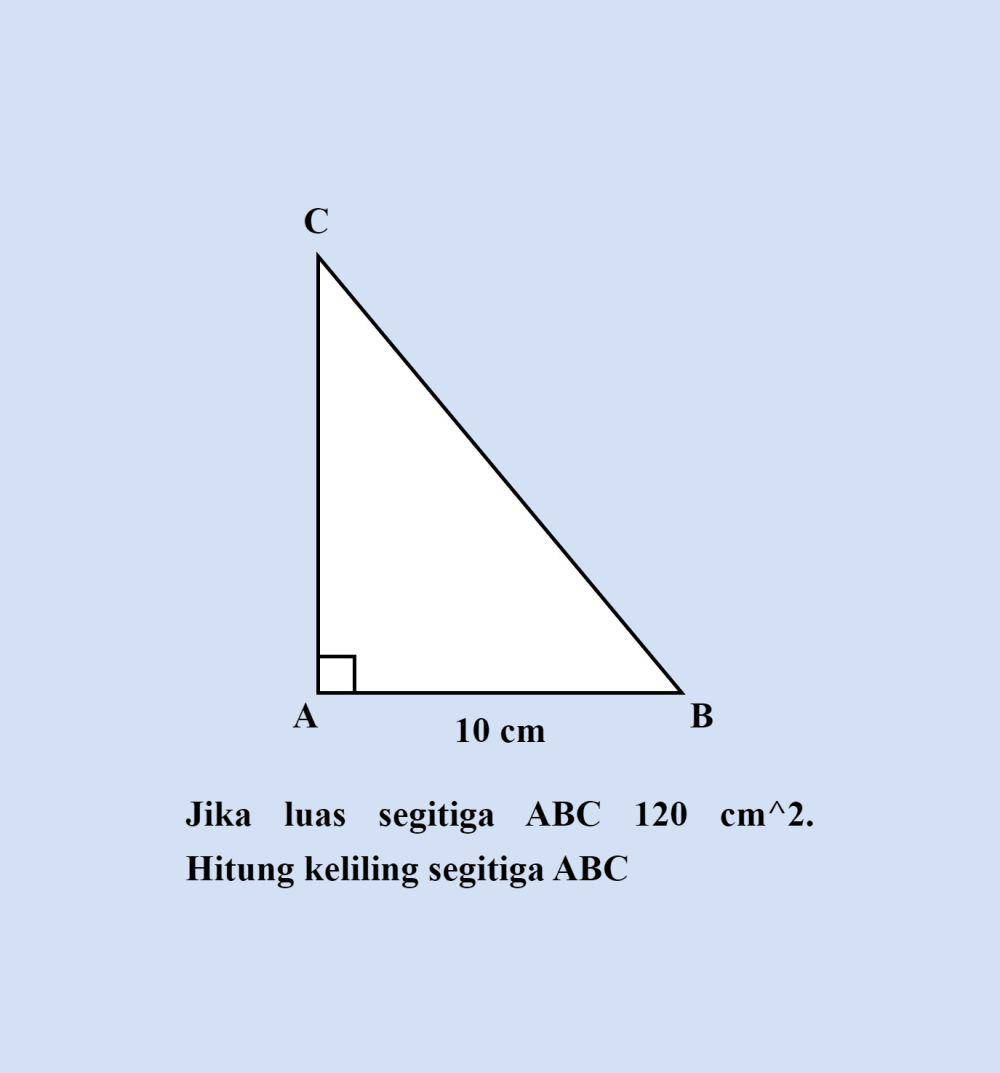
Pembahasan:
Diketahui:
AB = 10 cm
Luas segitiga ABC = 120 cm²
Ditanya:
Keliling segitiga ABC = ?
Jawaban:
Langkah pertama yang harus dilakukan adalah mencari tinggi segitiga (AC). Tinggi segitiga dapat ditemukan dengan memanfaatkan nilai luas dan alas yang sudah diketahui.
Luas = ½ x alas x tinggi
120 = ½ x 10 x AC
120 x 2 = 10 x AC
240 = 10AC
AC = 240 : 10
AC = 24
jadi tinggi segitiga ABC adalah 24 cm.
Langkah berikutnya adalah mencari panjang hipotenusa atau sisi miring segitiga ABC. untuk mencarinya kita dapat menggunakan rumus teorema Pythagoras.
c² = a² + b²
BC² = AB² + AC²
BC² = 10² + 24²
BC² = 100 + 576
BC² = 676
BC = 26
Jadi panjang BC adalah 26 cm.
Langkah terakhir adalah menghitung keliling segitiga ABC.
Keliling segitiga ABC = a + b + c
Keliling segitiga ABC = AB + AC + BC
Keliling segitiga ABC = 10 + 24 + 26
Keliling segitiga ABC = 60
Jadi keliling segitiga ABC ada 60 cm.
Tidak terlalu rumit, bukan? Semoga pembahasan ini memberikan kontribusi positif untuk menambah wawasan dan pemahaman kalian tentang segitiga siku-siku. Untuk memastikan pemahaman, silahkan kalian coba kerjakan ulang tiga soal di atas, lalu bandingkan jawaban kalian dengan jawaban yang ada di artikel ini. Selamat belajar dan terus semangat mencoba!