Apakah √16 adalah bilangan rasional?
√16 = 4
Bilangan Rasional: Pengertian, Sifat, dan Contoh Soal

Dalam matematika, ada banyak bentuk bilangan. Contohnya, ganjil dan genap, serta bilangan rasional dan irasional. Semuanya diperlukan dalam operasi hitung matematika.
Namun, apa itu bilangan rasional dan irasional? Cari tahu pengertian, perbedaan, contoh, hingga tips mengerjakan soalnya, yuk!
Bilangan rasional dan irasional
Apa itu bilangan rasional? Sebuah bilangan masuk kategori rasional apabila bilangan tersebut bisa diubah menjadi pecahan biasa (a/b). Syarat lainnya, apabila bilangan diubah menjadi desimal, lalu angkanya akan berhenti atau membuat pola bilangan.
Dalam kategori bilangan rasional, terdapat kelompok bilangan lain, yakni bilangan asli, bilangan cacah, bilangan prima, dan lain sebagainya. Menariknya, sebuah bilangan bisa diuji apakah termasuk bilangan rasional atau tidak. Pengujiannya dengan dengan mengubahnya ke pecahan atau desimal sebagaimana syarat bilangan rasional.
1. Mengubah bentuk menjadi pecahan biasa (a/b)
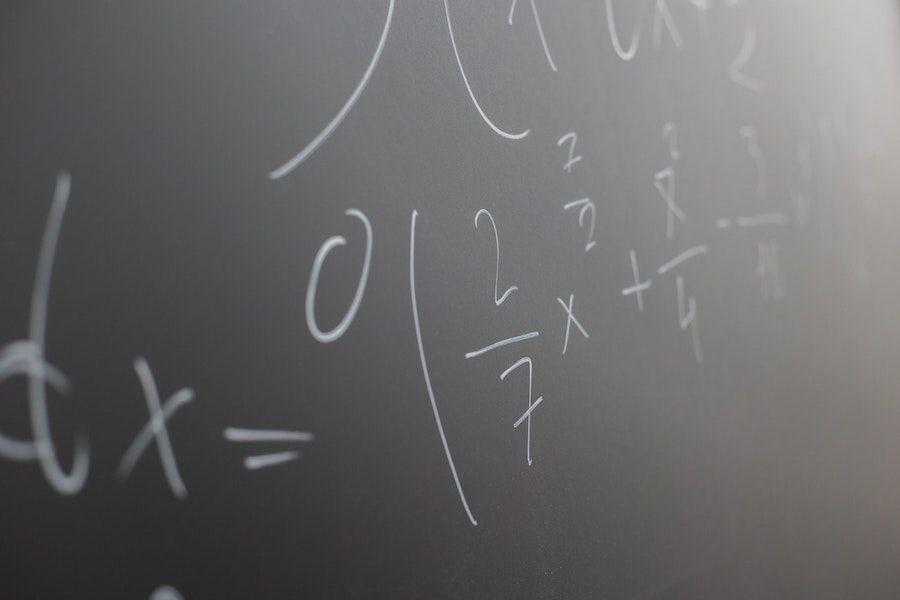
Cara pertama untuk membuktikan bilangan termasuk rasional atau tidak yakni dengan mengubahnya ke pecahan biasa. Pecahan a/b dengan posisi a sebagai pembilang dan b adalah penyebut.
Ketika sebuah bilangan diubah menjadi bentuk pecahan, lalu ‘a serta b’ alias pembilang dan penyebut bukan nol (0), maka dikatakan sebagai bilangan rasional. Contohnya seperti ini:
Jika 4 diubah ke pecahan, maka menjadi 4/1. Pembilang dan penyebutnya sama-sama bukan nol (0). Maka, √16 termasuk bilangan rasional.
2. Mengubah bentuk menjadi pecahan desimal (0,000)

Teorema bilangan rasional yang diubah ke desimal diuraikan sebagai berikut:
Dikatakan bilangan rasional apabila pecahan desimalnya berakhir (terbatas) atau desimalnya periodik (berpola).
Artinya, sebuah angka harus berakhir jelas atau mengulang, tetapi dengan pola. Jika demikian, angkat tersebut bisa masuk kategori bilangan rasional. Begini contohnya:
Apakah 0,121111111… adalah bilangan rasional?
Sekilas, kamu pasti bisa melihat bahwa angkanya tidak berhenti, tetapi memiliki pola. Namun, mari kita buktikan apakah itu termasuk bilangan rasional atau bukan.
Karena x= 0,121111111…
Coba kalikan dengan 1000 untuk mendapat persamaan pertama, yakni:
1000x = 121,1111…
Lalu, coba kalikan dengan 100 untuk membuat persamaan kedua, menjadi:
100x = 12,11111…
Lanjut, coba ubah menjadi pecahan biasa guna membuktikan bilangan di atas adalah bilangan rasional.
1000x — 100x = 121,1111… — 12,1111…
900x = 109
x = 109/900
Baik pembilang maupun penyebutnya (a/b) ≠ 0, bukan? Maka, 0,121111111 adalah bilangan rasional.
Perbedaan bilangan rasional dan irasional
Setelah membahas karakteristik bilangan rasional, lantas apa bedanya bilangan irasional? Dari uraian di atas diketahui bahwa sebuah bilang dikatakan irasional apabila tidak memenuhi syarat rasional.
Bilangan tersebut memiliki pembilang atau penyebut (a/b) = 0
Bilangan desimalnya berhenti, tetapi juga tidak memiliki pola.
Contohnya, nih:
5/7 = 0,714285714
Bilangan 5/7 yang dijadikan desimal tidak membentuk pola dan tidak berhenti. Artinya, bilangan tersebut merupakan bilangan irasional.
Sifat-sifat bilangan rasional

Bilangan rasional mempunyai sifat yang menjadi ciri-cirinya. Termasuk (a/b) ≠ 0 yang tadi sudah dipelajari, ya. Selanjutnya, ada sifat lain dari bilangan rasional, yakni:
- Berifat tertutup, artinya jika bilangan rasional dikalikan dengan bilangan rasional, maka yang terbentuk juga bilangan rasional.
- Komutatif berarti jika letak bilangan ditukar, akan tetap menghasilkan hasil hitung yang sama. Hal tersebut berlaku meski bilangan positif atau negatif.
- Asosiatif artinya,hasil dari penjumlahan tidak terpengaruh oleh di mana bilangan diletakkan. Sifat ini berlaku untuk perkalian maupun penjumlahan dalam operasi bilangan.
- Sifat distributif dari bilangan rasional dirumuskan dengan a/b . (c/d+e/f) = a/b . c/d + a/b . e/f.
- Perkalian dengan 0 (nol) sama dengan 0 (nol)
- Bentuk desimal yang berulang.
Contoh soal
Yuk, coba latihan soal supaya lebih paham! Berikut contoh soal dari konsep hingga praktik menentukan bilangan rasional.
Soal 1
Apa itu bilangan rasional?
A. Bilangan yang berbentuk bilangan negatif dan positif
B. Bilangan yang tidak dibagi dengan nol
C. Adalah bilangan yang bisa diubah menjadi pecahan biasa (a/b). Ketika diubah menjadi pecahan desimal, angkanya berhenti atau jika tidak, maka membentuk suatu pola pengulangan.
D. Bilangan yang tidak bisa diubah jadi pecahan biasa. Ketika menjadi pecahan desimal, angkanya tidak memiliki pola tertentu.
Jawabannya: C.
Soal 2
23 + 0,023 = ….
Penyelesaiannya menjadi:
Ubah 23 menjadi desimal. Misalnya dikali 1000, maka menjadi 23,000. Artinya:
23,000 + 0,023 = 23,023
Dengan demikian, hasilnya merupakan bilangan rasional.
Bilangan rasional cukup mudah untuk diidentifikasi, bukan? Pahami syarat pecahan biasa dan desimal, dengan begitu akan lebih mudah mengenali mana yang termasuk bilangan rasional ataupun irasional.





































![[QUIZ] Dari Jenis Galaksi yang Kamu Pilih, Ini Cara Kamu Melihat Masa Depan](https://image.idntimes.com/post/20250530/small-vecteezy-astrophotography-from-the-himalayas-2198639-small-097bb1575dfbb9113f53dc51ed222913-5196009990fdcf246e201234acb561c0.jpg)



![[QUIZ] Tebak Hewan yang Memiliki Gigitan Terkuat, Pernah Bertemu?](https://image.idntimes.com/post/20250417/788-06da9cb21925c208b6c5f4982411b31d-e48b6c2007ee46de724fcbed6735d9c1.jpeg)




