- Rumus simpangan kuartil data tunggal ganjil
Rumus Simpangan Kuartil: Contoh Soal dan Cara Mengerjakan

Rumus simpangan kuartil merupakan salah satu pembahasan dalam matematika statistika. Materi ini kerap muncul pada soal-soal ujian tingkat nasional, lho! Termasukdalam UTBK SBMPTN alias seleksi nasional masuk perguruan tinggi.
Kamu akan menemui materi ini secara berulang ketika duduk di bangku SMA. Biar makin mantap, yuk pelajari lagi serba-serbi simpangan kuartil dalam artikel ini!
Apa itu simpangan kuartil?

Simpangan kuartil dapat didefinisikan sebagai setengah dari perbedaan antara kuartil atas dan bawah. Nama lainnya yakni jangkauan semi antar-kuartil, deviasi kuartil, atau rentang semi-interkuartil.
Kuartil pertama dinamakan kuartil bawah (Q1). Adapun kuartil ketiga dinamakan sebagai kuartil atas (Q3). Simpangan kuartil sendiri dilambangkan dengan simbol Qd. Misalnya, ada 10 data, maka kuartil satunya berada di angka 3, kuartil dua di angka 5, dan kuartil tiga di angka 8. Adapun Qd-nya bisa dihitung menggunakan rumus.
Untuk menghitung simpangan kuartil, ada rumusnya. Formula hitungnya pun dibedakan antara data tunggal dan data kelompok. Di dalam data tunggal, terbagi lagi menjadi data tunggal genap dan ganjil. Lebih lengkapnya, dibahas di bawah, ya!
Rumus simpangan kuartil
Sebelum lanjut memahami rumusnya, penting untuk mengetahui perbedaan data tunggal dan data kelompok dulu. Data tunggal merupakan data yang disajikan secara sederhana, tidak mengandung interval, dan jumlahnya tidak terlalu banyak.
Sementara itu, data kelompok merupakan data yang telah disusun dalam bentuk interval. Misalnya, 1 sampai 5, 6 sampai 10, dan seterusnya. Jumlahnya pun lebih banyak dan biasanya langsung terbentuk dalam tabel frekuensi. Masing-masing bentuk data ini punya rumusnya sendiri-sendiri.
Rumus simpangan kuartil data tunggal
Seperti disebutkan sebelumnya, rumus kuartil data tunggal terbagi menjadi dua. Tergantung jumlah data disajikan atau yang tersedia. Misalnya, jumlah data atau (n) ada 8 berarti termasuk data genap.

Kamu perlu memperhatikan soal sebelum memilih rumus untuk mengerjakannya. Selain ganjil genap, perhatikan apakah hasil n+1 bisa habis dibagi 4 atau tidak. Selanjutnya, baru pilih rumus yang sesuai. Sebelah kiri merupakan rumus n+1 habis dibagi 4, sebelah kanan sebaliknya.
- Rumus simpangan kuartil data tunggal genap

Sama seperti data tunggal ganjil, pada data genap juga perlu diteliti apakah n alias jumlah data bisa dibagi 4 atau tidak. Sesuaikan rumusnya, ya.
Rumus simpangan kuartil data genap
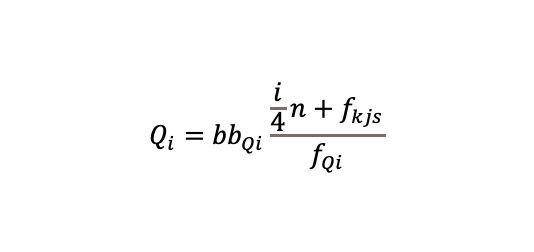
Dengan keterangan:
- Qi = kuartil ke-i
- bbQi = batas bawah kelas kuartil ke-i
- n = jumlah data
- fkjs = frekuensi kumulatif sebelum kelas kuartil ke-i
- fQi = frekuensi kelas kuartil ke-i
- p = panjang kelas
Contoh soal

Biar makin oke memahami rumus simpangan kuartil, langsung kita terapkan, yuk! Coba pahami contoh soal berikut ini, termasuk langkah-langkah penyelesaiannya.
Soal 1
Jika terdapat data sebanyak 123, berapa Q1, Q2, dan Q3-nya?
Jawab:
Kata kunci mengerjakan soal kuartil adalah mengerti bentuk jumlah datanya. Karena n=123, artinya n termasuk data ganjil. Ketika n+1, berarti menjadi 124 yang mana habis jika dibagi dengan angka 4. Maka, menggunakan rumus simpangan kuartil ganjil dengan n+1 habis dibagi 4. Menjadi:
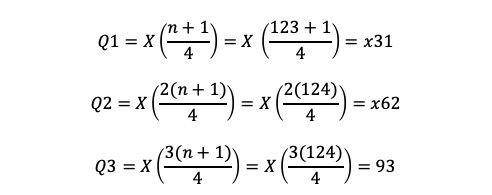
Maka, kuartil bawahnya adalah 31, sedangkan kuartil atasnya 93.
Soal 2
Perhatikan data tabel berikut. Tentukan nilai kuartilnya!
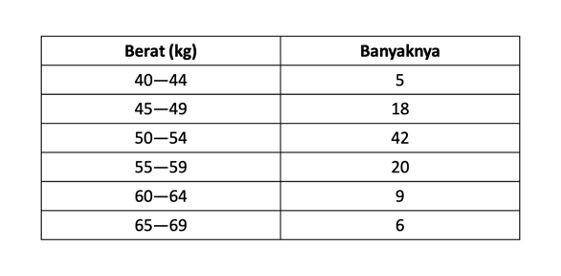
Bisa diketahui bahwa data yang ditanyakan merupakan data kelompok. Ini karena jumlah datanya banyak dan disajikan dalam bentuk tabel yang ada intervalnya. Maka, kamu bisa menghitungnya menggunakan rumus simpangan kuartil data kelompok, ya.
Pertama, kamu perlu mencari frekuensi kumulatif. Alias banyaknya data keseluruhan. Untuk mencarinya kamu bisa menggunakan tabel seperti di bawah ini.
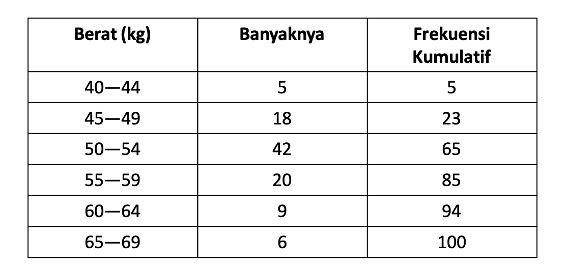
Setelah diketahui frekuensi kumulatifnya, kamu bisa mencari masing-masing kuartil bawah, tengah, dan atas. Caranya:
Q₁ = 1/4 x 100 = 25
Q₂ = 2/4 x 100 = 50
Q₃ = 3/4 x 100 = 75
Baru kemudian dimasukkan dalam rumus simpangan kuartil data kelompok. Menjadi:
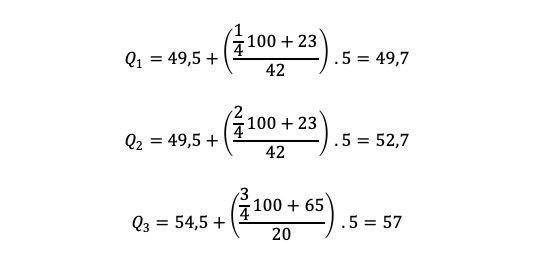
Dari penghitungan di atas, bisa diketahui bahwa kuartil bawahnya adalah 49,7 dan kuartil atasnya 57. Sementara Q2-nya adalah 52,7.
Gimana, sudah bisa memahami pembahasan rumus simpangan kuartil di atas? Tidak apa-apa kalau belum, kamu bisa mempelajarinya perlahan-lahan. Semangat!














































