Simpangan Rata-Rata: Rumus, Cara Menghitung, dan Contoh Soal
ilustrasi matematika (unsplash.com/anniespratt)
Follow IDN Times untuk mendapatkan informasi terkini. Klik untuk follow WhatsApp Channel & Google News
Simpangan rata-rata merupakan salah satu pembahasan dalam sub-bab statistik. Ilmu ini diajarkan pada mata pelajaran matematika. Materi ini penting, karena dipakai untuk mengetahui seberapa besar penyimpangan dan area persebaran pada data-data statistik.
Rumus simpangan rata-rata ada dua jenis. Pertama, untuk data tunggal dan kedua untuk data berkelompok. Apa bedanya dan bagaimana cara menghitungnya? Yuk, belajar sama-sama dari artikel ini!
Apa itu simpangan rata-rata?
Simpangan rata-rata juga disebut sebagai deviasi mean atau simpangan rata-rata merupakan nilai rata-rata dari selisih setiap data dengan nilai mean atau rataan hitungnya. Penggunaan simpangan rata-rata juga menjadi bagian dari cara mencari ukuran penyebaran data, seperti simpangan baku alias standar deviasi. Seperti disebutkan pada pembuka, simpangan rata-rata digunakan untuk mengetahui seberapa jauh nilai menyimpang serta bagaimana persebaran data hendak diolah.
Rumus simpangan rata-rata
Dari mana kita bisa mencari nilai simpangan rata-rata? Caranya, dengan menjumlah semua nilai mutlak simpangan, lalu bagi dengan banyaknya nilai data. Adapun rumus simpangan baku terbagi dua, berikut lebih lengkapnya.
Rumus simpangan rata-rata data tunggal
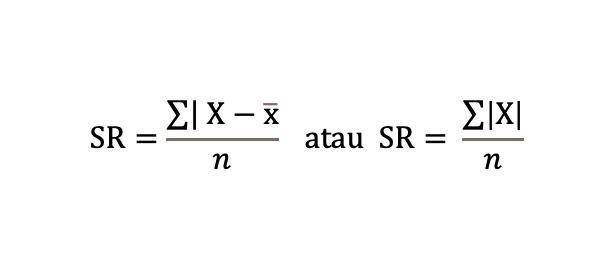
ilustrasi rumus simpangan rata-rata data tunggal (IDN Times/Laili Zain)Keterangan:
- SR = simpangan rata-rata
- X = data ke-i, ada juga yang menyimbolkan dengan xi
- x dengan aksen garis di atas = nilai rata-rata data
- n = banyak data
Coba kita praktikkan rumus langsung ke dalam contoh soal, ya.
Simpangan rata-rata dari data 9, 3, 7, 8, 4, 5, 4, 8 adalah?
Diketahui:
- n = 8
Kita perlu mencari x dengan aksen garis di atasnya alias nilai rata-rata datanya dahulu, Guys. Caranya dengan membagi jumlah seluruh data dengan banyaknya data.
Jadi:
x aksen = 9 + 3 + 7 + 8 + 4 + 5 + 4 + 8 : 8
x aksen = 48 : 8 = 6
Maka, x aksen = 6
Lanjut, baru kita bisa mencari simpangan rata-rata sebagaimana pada gambar berikut:
Editor’s picks
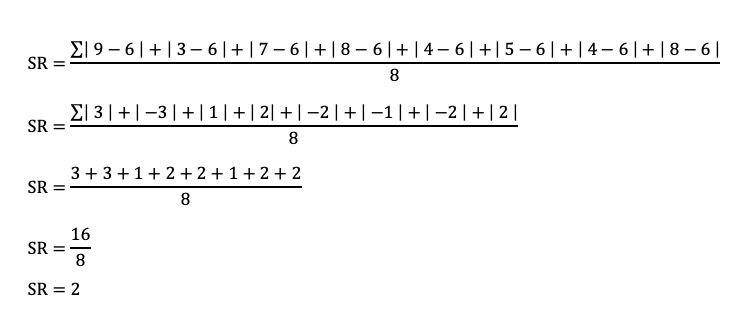
ilustrasi penyelesaian soal simpangan rata-rata data tunggal (IDN Times/Laili Zain)Jadi, simpangan rata-rata dari data tunggal di atas adalah 2. Cukup mudah, bukan? Mirip dengan menghitung rata-rata pada umumnya.
Baca Juga: Rumus Pythagoras dan Contohnya, Mudah Dipelajari Kok!
Rumus simpangan rata-rata data kelompok
Bagaimana dengan data kelompok? Untuk data tersebut, kamu tidak bisa menggunakan rumus jika yang dicari simpangan rata-ratanya termasuk data kelompok. Tepatnya, data dengan jumlah banyak yang disajikan dalam bentuk tabel frekuensi. Ada rumus khusus untuk menyelesaikan soal data kelompok sebagai berikut.
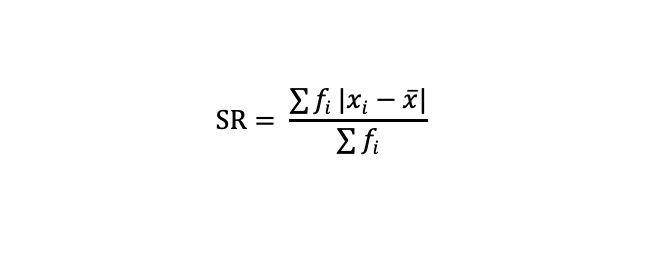
ilustrasi rumus simpangan data rata-rata data kelompok (IDN Times/Laili Zain)Keterangan:
- SR = simpangan rata-rata
- xi = data ke-i
- x aksen = nilai rata-rata data
- fi atau f = total frekuensi data
Langsung saja kita terapkan rumus ke soal di bawah ini, yuk. Coba cari simpangan rata-rata dari data berikut:
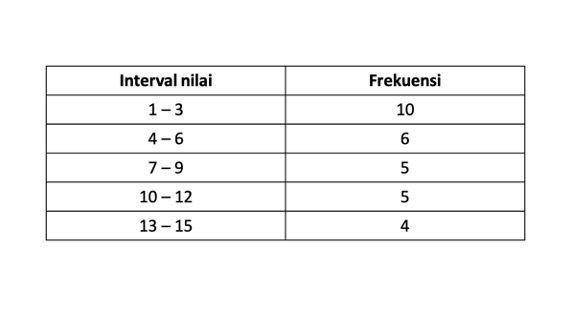
ilustrasi soal simpangan rata-rata data kelompok (IDN Times/Laili Zain)Untuk bisa mencari simpangan rata-rata dari data di atas, kamu perlu mencari tahu dulu nilai tengah alias xi. Karena di akhir kamu memerlukan nilai x aksen yang didapat dari xi dikali fi. Maka, tabelnya menjadi:
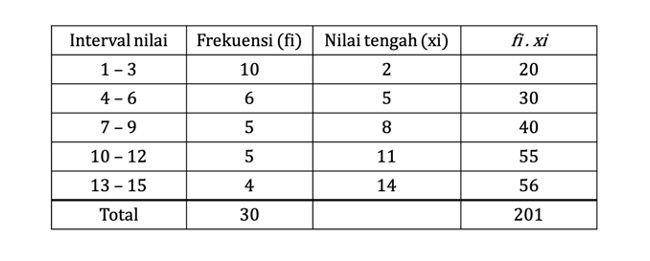
ilustrasi mencari simpangan rata-rata data kelompok (IDN Times/Laili Zain)Lanjut, x aksen bisa dicari menggunakan rumus:
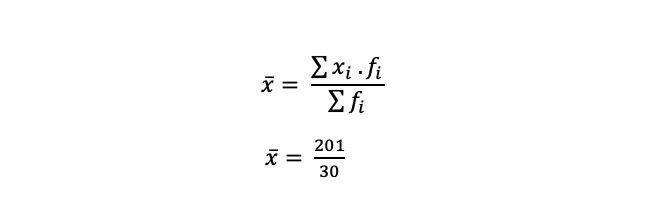
ilustrasi menghitung simpangan rata-rata data kelompok (IDN Times/Laili Zain)Hasilnya yakni 6,7. Selanjutnya, kita perlu mencari simpangan rata-rata dari masing-masing interval data untuk menentukan Σfi xi-x aksenpada rumus. Caranya:
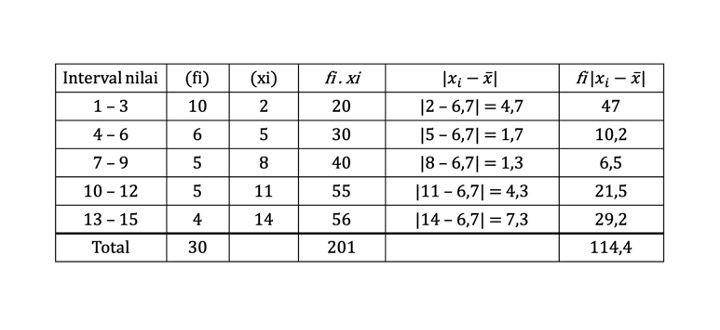
ilustrasi mencari simpangan rata-rata data kelompok (IDN Times/Laili Zain)Terakhir, tinggal masukkan hasilnya ke rumus awal mencari simpangan rata-rata.
SR = 114,4 : 30 = 3,81
Cukup pusing mencari simpangan rata-rata? Walau pusing, tapi tetap harus belajar, sebab materi ini akan terus digunakan, lho! Terlebih saat di bangku perkuliahan untuk menguji data penelitian.
Baca Juga: Rumus Luas Permukaan Bola: Cara Menghitung dan Contoh Soal
Topik:
Berita Terkini Lainnya
