Himpunan: Pengertian, Cara Menyatakan, dan Operasi Himpunan
Himpunan adalah salah satu istilah yang dipakai dalam menjelaskan materi matematika. Tentunya, kamu sudah tidak asing dengan istilah ini di bangku sekolah. Himpunan sendiri merujuk pada sekelompok objek yang dianggap satu kesatuan.
Nah, materi himpunan umumnya akan mulai dipelajari dari jenjang pendidikan menengah pertama (SMP). Untuk penjelasan terkait pengertian himpunan, cara menyatakan, dan jenis-jenisnya, mari simak ulasannya berikut ini.
1. Pengertian himpunan
Himpunan adalah sekumpulan objek yang memiliki sifat yang dapat didefinisikan dengan jelas yang dianggap sebagai satu kesatuan. Dalam ilmu matematika, teori himpunan baru diciptakan di akhir abad ke-19, lho!
Teori ini diciptakan untuk menjelaskan matematika modern. Dikutip dari laman Zenius.net, himpunan yakni bentuk sekumpulan benda atau objek yang anggotanya bisa didefinisikan dan ditentukan secara jelas.
Selain itu, himpunan merupakan sekumpulan obyek yang terukur serta diketahui anggota-anggota dalam himpunan tersebut. Dalam himpunan ada “anggota himpunan” dan “bukan himpunan", yang anggotanya tidak bisa ditentukan dengan jelas dan tidak bisa diukur.
2. Cara menyatakan himpunan
Secara umum, himpunan disimbolkan dengan huruf kapital dan anggota himpunan berupa huruf maka dituliskan dengan huruf kecil. Berikut ini beberapa cara menyatakan penulisan himpunan. Yuk, cek di bawah ini!
- Kata-kata, yakni menyebutkan semua syarat dari anggota himpunan tersebut di dalam kurung kurawal.
Contoh: D adalah himpunan bilangan genap antara 4 dan 20, maka bisa dituliskan dituliskan menjadi D = {bilangan genap antara 4 dan 20} - Notasi pembentuk himpunan, yakni menyebutkan semua sifat dari anggota himpunan dengan anggotanya yang dinyatakan dalam suatu variabel dan dituliskan di dalam kurung kurawal.
Contoh: D merupakan himpunan bilangan genap antara 4 dan 20, maka bisa dituliskan menjadi D = {x | 4 < x < 20, x Є bilangan genap} - Mendaftar anggota-anggotanya, yakni menuliskan semua anggota dari himpunan tersebut di dalam kurung kurawal dengan dibatasi tanda koma di antara anggotanya. Jika anggota dari himpunan tersebut terlalu banyak, bisa menuliskan dengan “…”. Contoh: D merupakan himpunan bilangan genap antara 4 dan 20, maka bisa dituliskan menjadi D = {6, 8, 10, 12, 14, 16, 18}
3. Operasi himpunan
Setelah memahami terkait pengertian dan cara menyatakan, berikut ini operasi himpunan yang wajib untuk disimak. Adapun operasi himpunan tersebut adalah sebagai berikut.
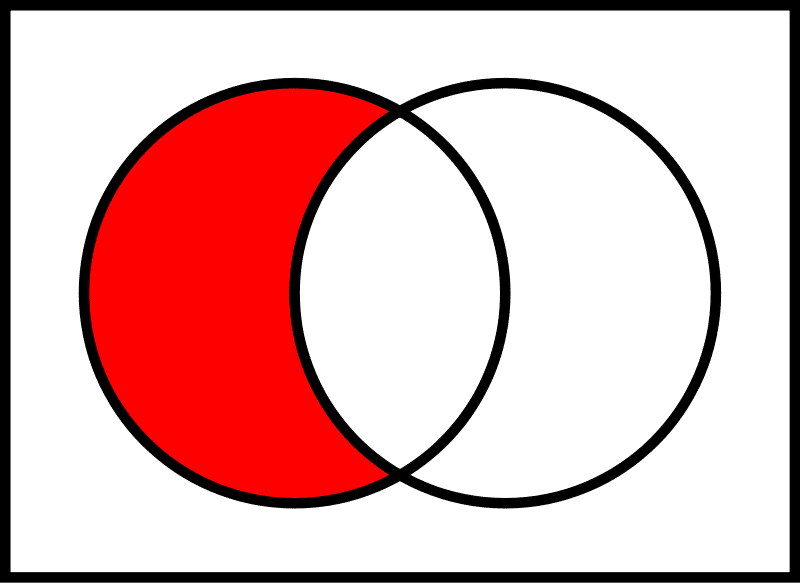
1) Irisan
Irisan dari dua himpunan X dan Y adalah himpunan yang anggotanya ada di himpunan X dan juga di himpunan Y. Irisan antara dua buah himpunan ini dinotasikan oleh tanda “∪”.
Contoh:
X = {1,2,3,4}
Y = {2,3,5,6}
Maka X∪Y = {1,2,3,4,5,6}
2) Selisih
X selisih Y adalah himpunan dari anggota X yang tidak memuat anggota Y. Selisih antara dua buah himpunan ini dinotasikan dengan tanda “-“.
Contoh:
X = {1,2,3,4}
Y= {2,3,5,6}
Maka A – B = {1,4}
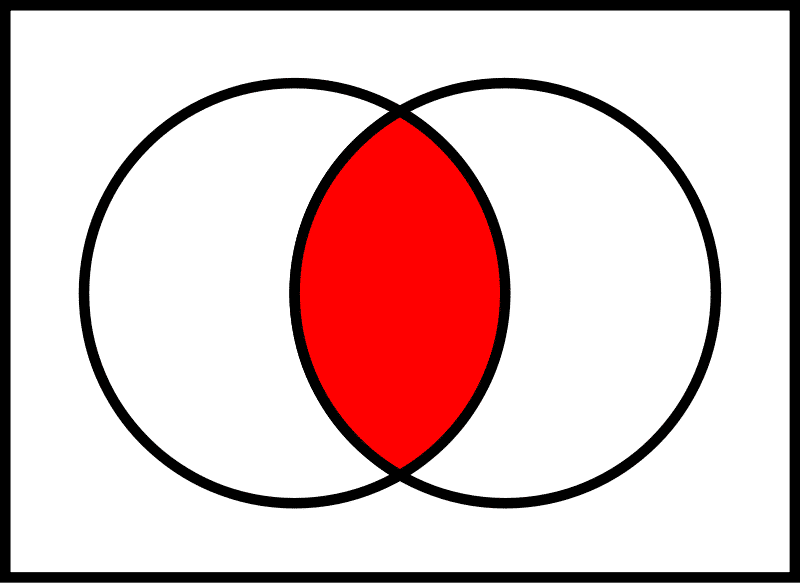
3) Komplemen
Komplemen suatu himpunan adalah himpunan lain yang memuat semua anggota semesta yang tidak dimiliki oleh himpunan tersebut. Komplemen A dinotasikan dengan AC.
Contoh:
A = {a, d, f, h}
S = {a, b, c, d, e, f, g, h, i}
Maka AC = {b, c, e, g, i}
Nah, itulah pengertian, cara menyatakan, dan operasi himpunan yang pastinya kerap ditemui dalam materi matematika sejak di jenjang SMP. Himpunan adalah sekumpulan objek yang memiliki sifat yang bisa didefinisikan dengan jelas yang dianggap sebagai satu kesatuan.
