5 Latihan Menarik Menghitung Luas Segitiga Siku-Siku dan Solusinya!

Mari berlatih dengan serangkaian latihan soal menarik yang akan memperkaya pemahamanmu! Dalam artikel ini, terdapat lima latihan soal yang fokus pada cara menghitung luas segitiga siku-siku, dilengkapi dengan pembahasan yang terperinci.
Setiap soal akan membantumu untuk memperdalam pemahamanmu tentang cara menghitung luas segitiga siku-siku. Sebelum mengerjakan soal tersebut, mari mengingat kembali rumus menghitung luas segitiga. Rumusnya adalah sebagai berikut.
1. Rumus luas segitiga
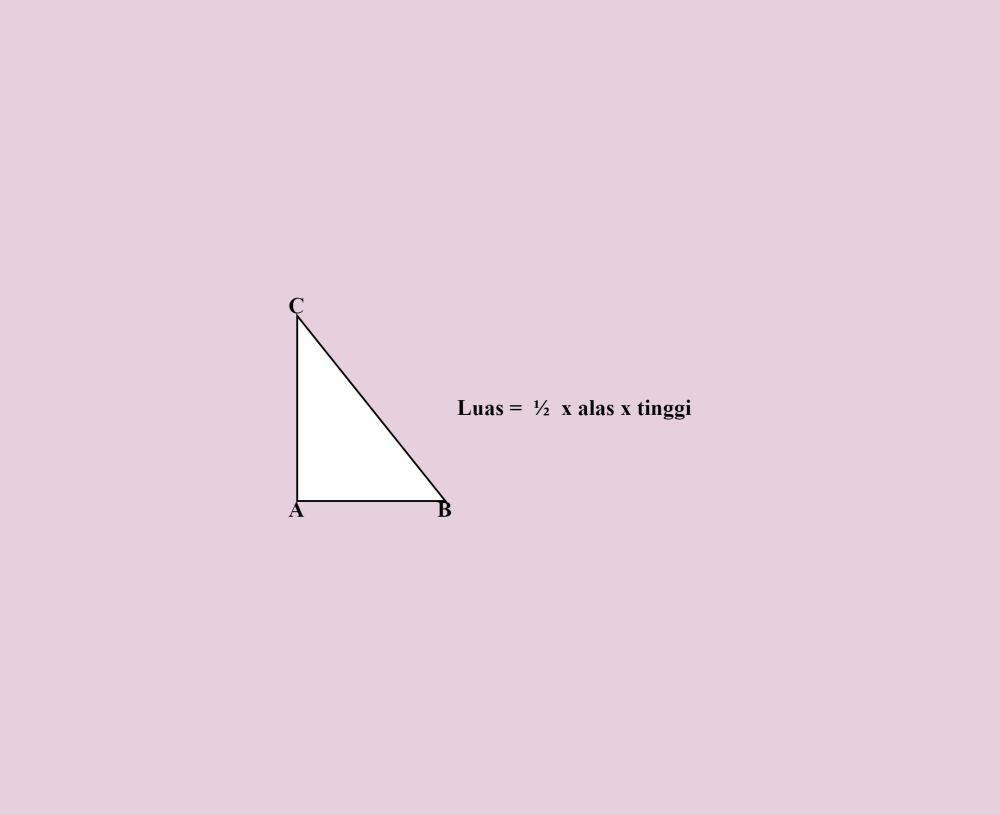
Contoh soal menghitung luas segitiga siku-siku dan pembahasannya
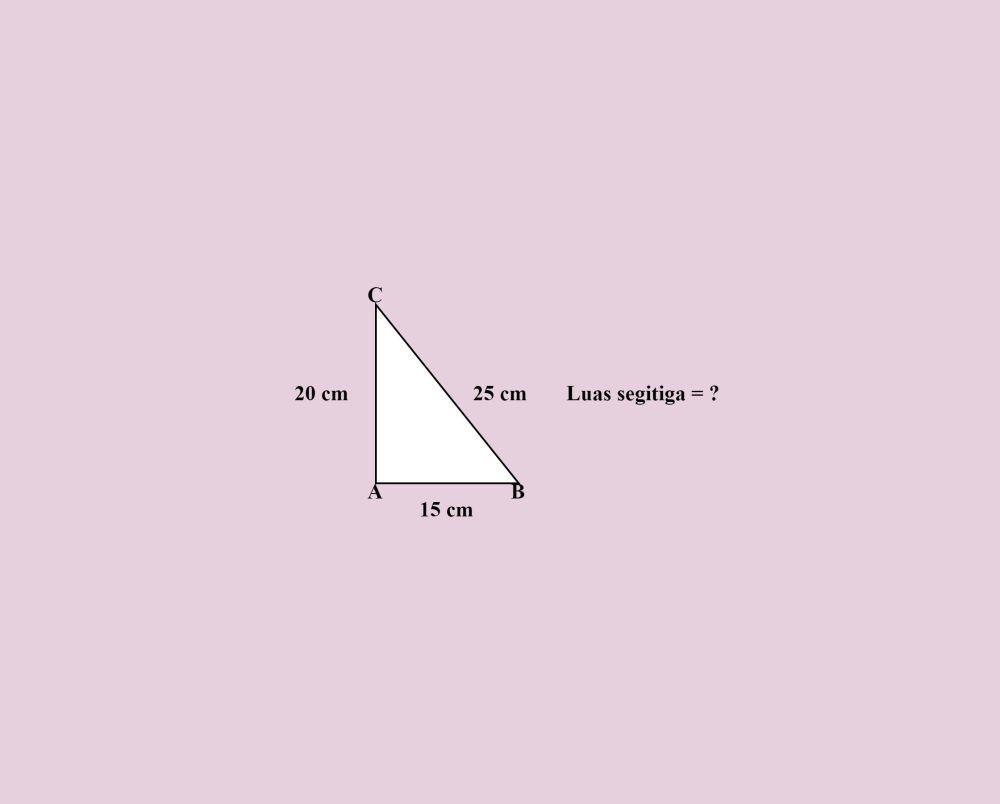
Hitunglah luas segitiga siku-siku ABC di atas!
Pembahasan:
Diketahui:
AB (alas) = 15 cm
AC (tinggi) = 20 cm
Ditanya:
Luas segitiga ABC = ?
Jawaban:
Luas segitiga ABC = ½ x alas x tinggi
Luas segitiga ABC = ½ x 15 x 20
Luas segitiga ABC = ½ x 300
Luas segitiga ABC = 150
Jadi luas segitiga siku-siku ABC adalah 150 cm².
2. Contoh soal menghitung luas segitiga siku-siku dan pembahasannya

Perhatikan gambar di atas. Jika luas segitiga siku-siku ABC = 24 cm² dan panjang AB = 6 cm, berapakah panjang AC?
Pembahasan:
Diketahui:
Luas segitiga = 24 cm²
AB = 6 cm
Ditanya:
AC = ?
Jawaban:
Untuk mencari panjang AC yang merupakan tinggi segitiga ABC, kita dapat memanfaatkan luas segitiga ABC yang sudah diketahui.
Luas segitiga = 24
½ x alas x tinggi = 24
½ x 6 x AC = 24
3 x AC = 24
AC = 24 : 3
AC = 8
Jadi panjang AC adalah 8 cm.
3. Contoh soal menghitung luas segitiga siku-siku dan pembahasannya
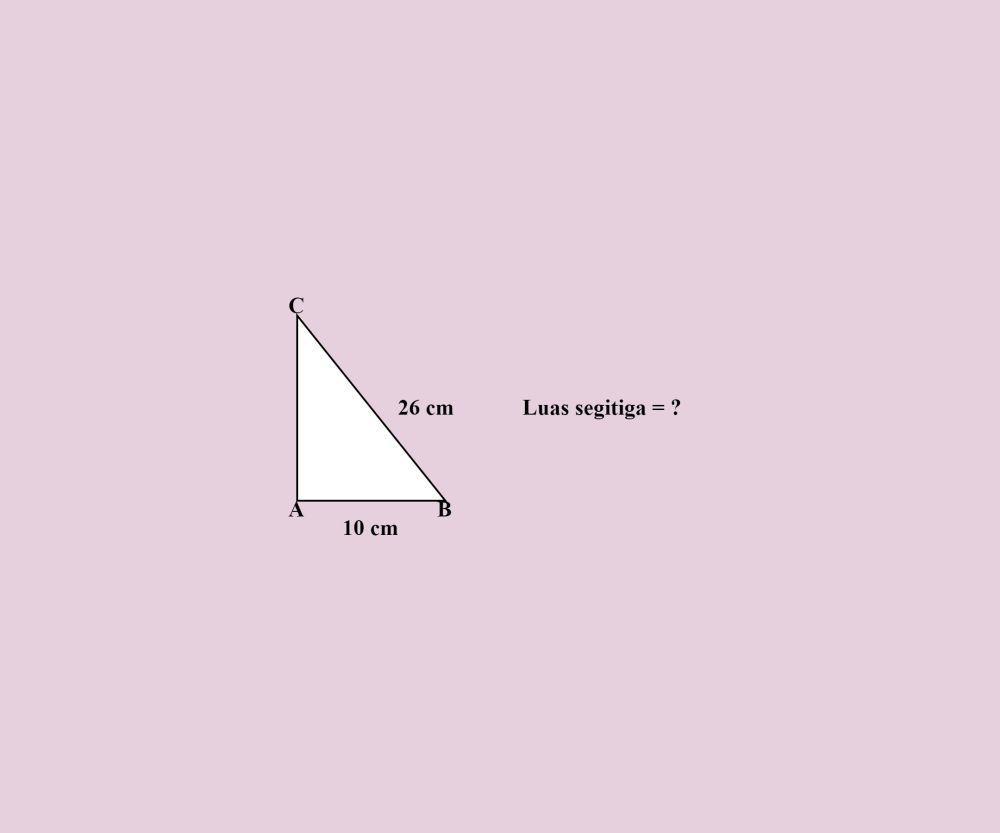
Perhatikan gambar di atas. Hitunglah luas segitiga tersebut!
Pembahasan:
Diketahui:
BC = 26 cm
AB = 10 cm
Ditanya:
Luas segitiga ABC = ?
Jawaban:
Untuk menghitung luas segitiga ABC kita perlu mencari panjang AC yang merupakan tinggi segitiga menggunakan rumus Pythagoras.
c² = a² + b²
BC² = AB² + AC²
AC² = BC² - AB²
AC² = 26² - 10²
AC² = 676 - 100
AC² = 576
AC = 24
Jadi panjang AC adalah 24 cm.
Luas segitiga ABC = ½ x alas x tinggi
Luas segitiga ABC = ½ x 10 x 24
Luas segitiga ABC = ½ x 240
Luas segitiga ABC = 120
Jadi luas segitiga siku-siku ABC adalah 120 cm².
4. Contoh soal menghitung luas segitiga siku-siku dan pembahasannya
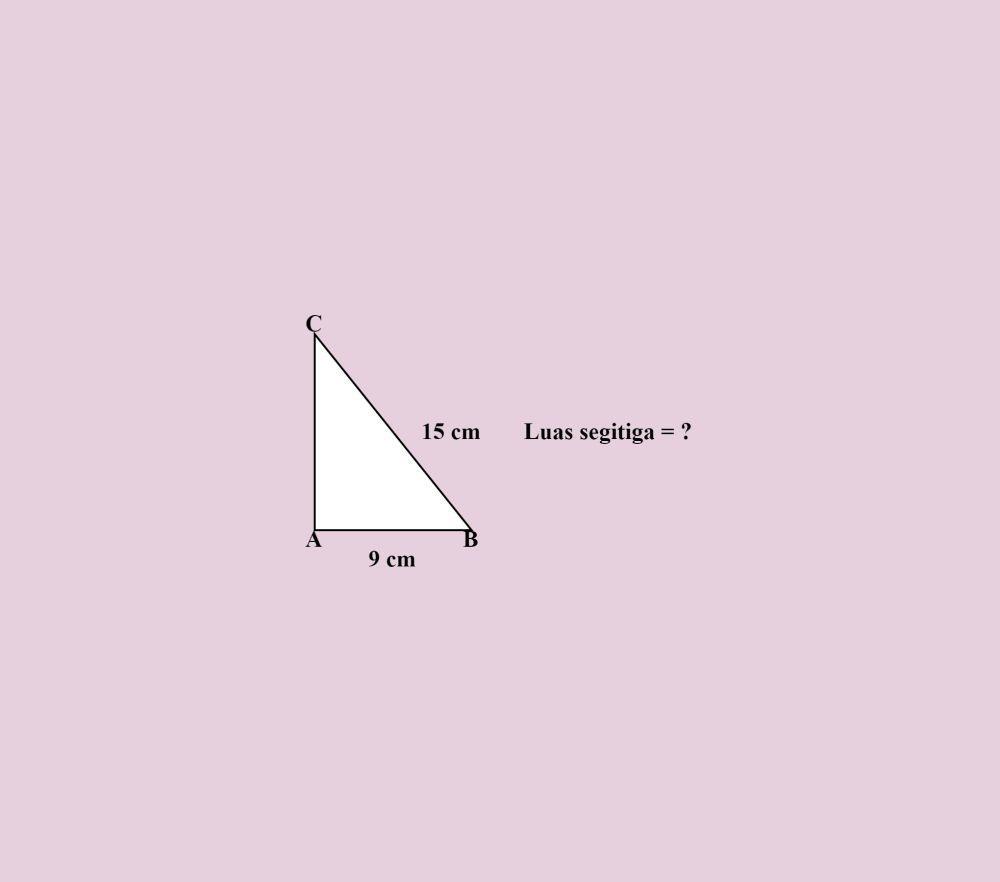
Berapakah luas segitiga siku-siku ABC di atas!
Pembahasan:
Diketahui:
AB = 9 cm
BC = 15 cm
Ditanya:
Luas segitiga ABC =?
Jawaban:
Untuk menghitung luas segitiga ABC kita perlu mencari panjang AC yang merupakan tinggi segitiga menggunakan rumus Pythagoras.
c² = a² + b²
BC² = AB² + AC²
AC² = BC² - AB²
AC² = 15² - 9²
AC² = 225 - 81
AC² = 144
AC = 12
Jadi panjang AC adalah 12 cm.
Luas segitiga ABC = ½ x alas x tinggi
Luas segitiga ABC = ½ x 9 x 12
Luas segitiga ABC = ½ x 108
Luas segitiga ABC = 54
Jadi luas segitiga siku-siku ABC adalah 54 cm².
5. Contoh soal menghitung luas segitiga siku-siku dan pembahasannya
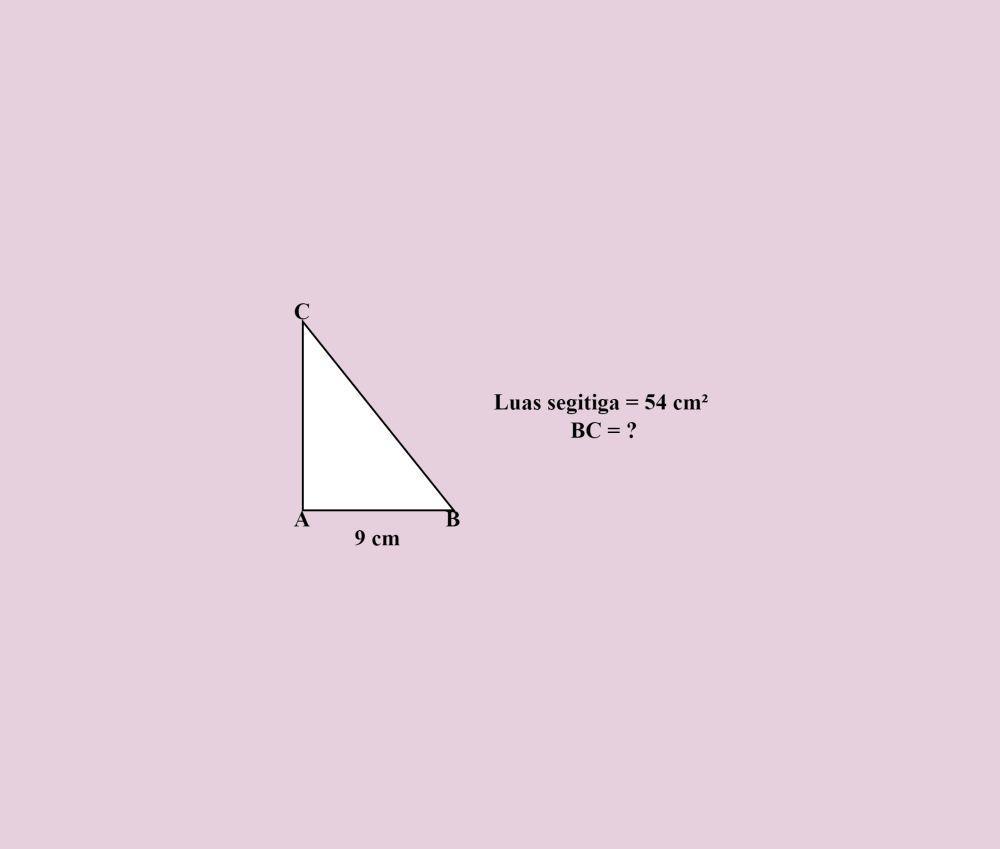
Perhatikan gambar di atas. Jika luas segitiga ABC = 54 cm² dan panjang AB = 9 cm, hitunglah panjang BC!
Pembahasan:
Diketahui:
Luas segitiga ABC = 54 cm²
AB = 9 cm
Ditanya:
BC = ?
Jawaban:
Untuk mencari panjang BC kita harus mencari panjang AC atau tinggi segitiga. Untuk mencari panjang AC kita dapat memanfaatkan luas segitiga ABC yang sudah diketahui.
Luas segitiga ABC = 54
½ x alas x tinggi = 54
½ x 9 x AC = 54
9 x AC = 54 x 2
9AC = 108
AC = 108 : 9
AC = 12
Jadi panjang AC adalah 12 cm.
Untuk mencari panjang BC kita dapat menggunakan rumus Pythagoras.
c² = a² + b²
BC² = AB² + AC²
BC² = 9² + 12²
BC² = 81 + 144
BC² = 225
BC = 15
Jadi panjang BC adalah 15 cm.
Nah itulah lima latihan soal untuk berlatih menghitung luas segitiga siku-siku lengkap dengan pembahasannya. Semoga soal latihan tersebut dapat menambah pemahamanmu tentang cara menghitung luas segitiga siku-siku. Kamu juga bisa mencoba mengerjakan kembali soal latihan di atas secara mandiri. Selamat mencoba dan semangat belajar!














































