5 Soal tentang Trapesium Beserta Pembahasannya, Wajib Disimak!
Dalam petualangan matematika kali ini, kita akan mempelajari materi yang menarik dan penuh tantangan berkaitan dengan bangun datar trapesium. Melalui serangkaian soal-soal seru, kita akan memecahkan misteri-misteri tersebut dan menemukan jawaban yang tepat. Siapkan pensil dan kertas, karena kita siap memulai perjalanan matematika yang mengasyikkan ini! Simak terus, ya!
1. Pengertian trapesium
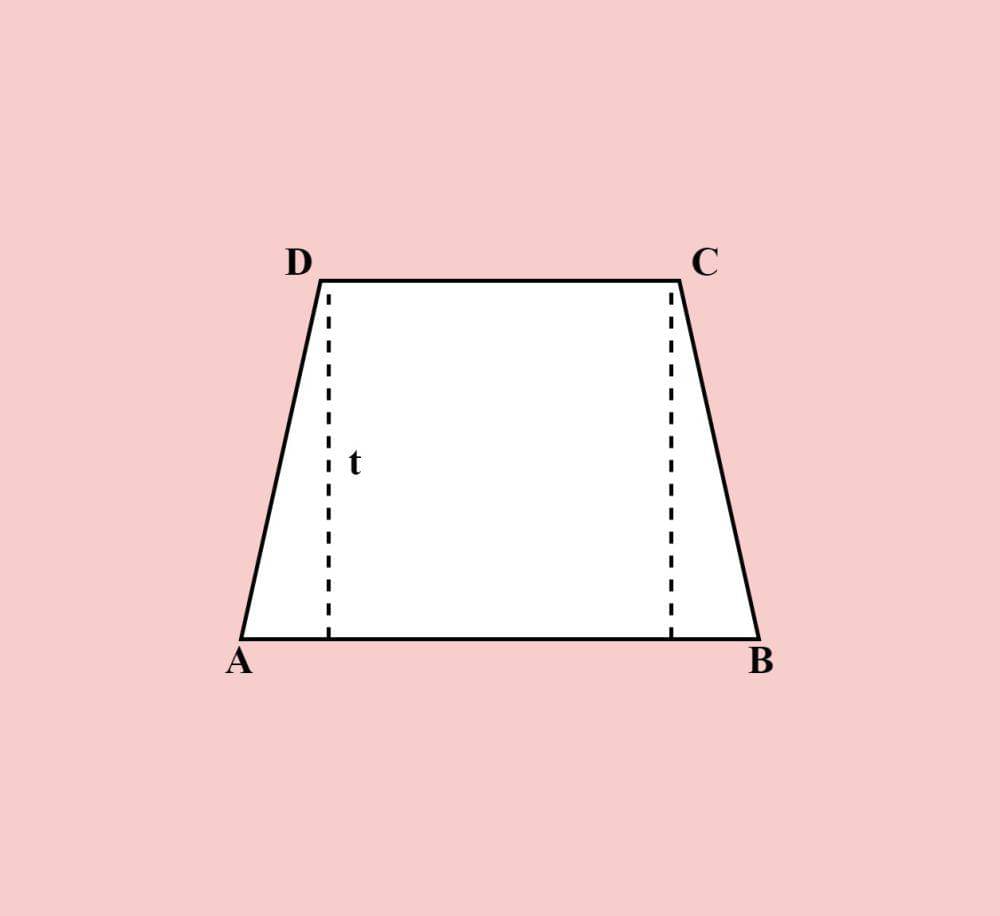
Trapesium adalah bangun datar segi empat yang memiliki empat rusuk, empat titik sudut, dan empat sisi dengan sepasang sisi yang berhadapan sejajar. Trapesium memiliki dua sudut lancip dan dua sudut tumpul serta satu simetri putar. Total sudut pada trapesium adalah 360 derajat. Dan jumlah sudut yang berdekatan (sudut sepihak) di antara dua sisi sejajar adalah 180 derajat.
Trapesium juga memiliki garis tinggi (t) yang dapat ditarik tegak lurus dari salah satu ujung sisi sejajar ke garis yang menghubungkan sisi sejajar tersebut. Garis tinggi ini berguna untuk mengukur jarak antara sisi sejajar dan memainkan peran penting dalam perhitungan luas trapesium.
2. Rumus luas dan keliling trapesium
Berikut ini adalah rumus luas dan keliling dari trapesium:
- Rumus luas trapesium
Untuk menghitung luas trapesium rumusnya adalah sebagai berikut:
Luas trapesium = ½ x (jumlah sisi sejajar) x tinggi = ½ (alas (AB) + atap (DC)) x tinggi; - Rumus keliling trapesium
Untuk menghitung keliling trapesium rumusnya adalah sebagai berikut:
Keliling trapesium = alas + atap + kaki1 + kaki2 = AB + DC + AD + BC.
3. Contoh soal pertama dan pembahasannya
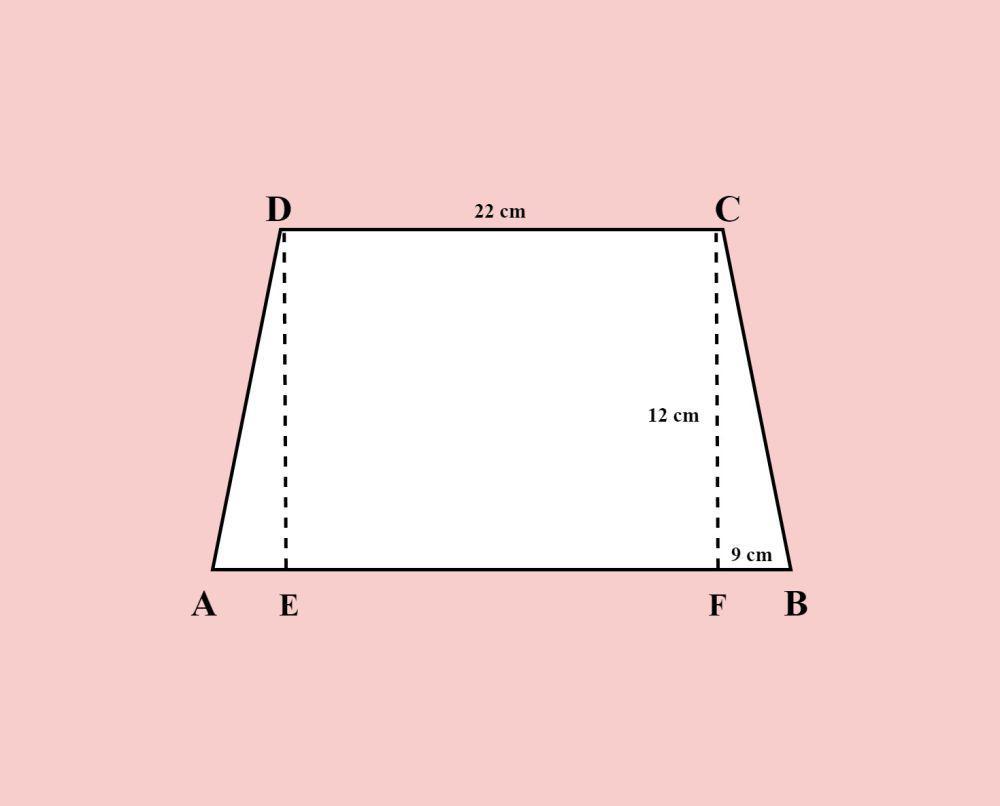
Perhatikan gambar di atas. Hitunglah keliling trapesium.
Pembahasan:
Pengingat: Sebelum menjawab soal matematika, biasakan untuk mencatat semua informasi yang ada di soal, ya! Hal itu akan sangat membantu kita dalam menemukan jawaban yang tepat.
Diketahui:
Atap trapesium => DC = 22 cm
DC = EF = 22 cm
BF = AE = 9 cm
Tinggi trapesium => ED = FC = 12 cm
Alas trapesium => AB = (AE + EF + BF) = (9 + 22 + 9) = 40 cm
Rumus keliling trapesium = alas + atap + kaki1 + kaki2 = AB + DC + AD + BC
Trapesium ABCD adalah trapesium sama kaki maka panjang kaki1 = panjang kaki2
Ditanya:
Keliling trapesium = ?
Jawaban:
Langkah pertama: mencari panjang AD (kaki1) dan BC (kaki2).
Karena trapesium ABCD adalah trapesium sama kaki, sehingga terdapat dua segitiga siku-siku yaitu BFC dan AED yang memiliki panjang sisi bawah, sisi tegak, dan sisi miring yang sama.
BF = AE = 9 cm
FC = ED = 12 cm
Maka AD = BC
Panjang sisi miring segitiga = panjang sisi miring atau kaki trapesium
Maka untuk mencari panjangnya kita dapat menggunakan rumus teorema Pythagoras:
c² = a² + b²
AD² = AE² + ED²
AD² = 9² + 12²
AD² = 81 + 144
AD² = 225
AD = 15
Jadi, AD = BC = 15 cm
Langkah kedua: menghitung keliling trapesium.
Keliling trapesium = alas + atap + kaki1 + kaki2
Keliling trapesium = AB + DC + AD + BC
Keliling trapesium = 40 + 22 + 15 + 15
Keliling trapesium = 92 cm
Jadi keliling trapesium tersebut adalah 92 cm.
4. Contoh soal kedua dan pembahasannya
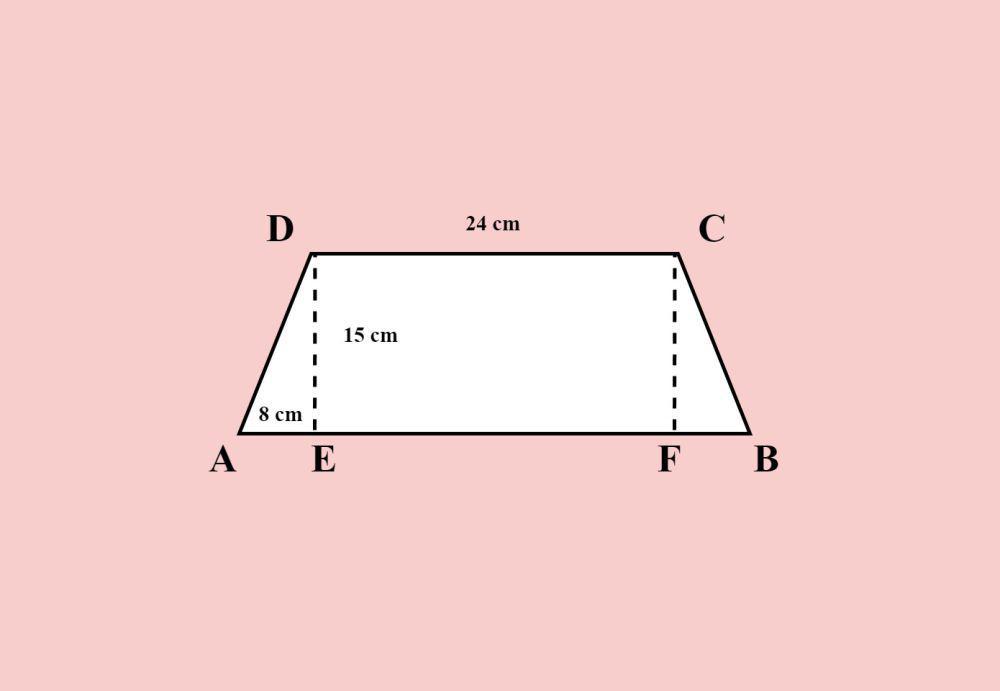
Perhatikan gambar di atas.
Luas bangun trapesium tersebut adalah…
Pembahasan:
Diketahui:
AE = BF = 8 cm
DC = EF = 24 cm
DE = CF = 15 cm
AB = AE + EF + BF = 8 + 24 + 8 = 40 cm
Rumus luas trapesium = ½ x (jumlah sisi sejajar) x tinggi = ½ (alas (AB) + atap (DC)) x tinggi
Ditanya:
Luas trapesium = ?
Jawaban:
Luas trapesium = ½ x (jumlah sisi sejajar) x tinggi
Luas trapesium = ½ (AB + DC) x DE
Luas trapesium = ½ (40 + 24) x 15
Luas trapesium = ½ (64) x 15
Luas trapesium = 32 x 15
Luas trapesium = 480 cm²
Jadi luas trapesium adalah 480 cm².
5. Contoh soal ketiga dan pembahasannya
Perhatikan gambar di atas.
Luas trapesium tersebut adalah…
Pembahasan:
Diketahui:
BF = AE = 5 cm
DC = EF = 20 cm
BC = AD = 13 cm
AB = AE + EF + BF = 5 + 20 + 5 = 30 cm
Trapesium ABCD adalah trapesium sama kaki
Rumus luas trapesium = ½ x (jumlah sisi sejajar) x tinggi = ½ (alas (AB) + atap (DC)) x tinggi
Ditanya:
Luas trapesium = ?
Jawaban:
Langkah pertama: mencari tinggi trapesium.
Karena trapesium ABCD adalah trapesium sama kaki, sehingga terdapat dua segitiga siku-siku yaitu BFC dan AED yang memiliki panjang sisi bawah, sisi tegak, dan sisi miring yang sama.
BF = AE = 5 cm
AD = BC = 13 cm
Maka FC = ED
Panjang sisi tegak segitiga = tinggi trapesium
Maka untuk mencari panjangnya kita dapat menggunakan rumus teorema Pythagoras:
c² = a² + b²
AD² = AE² + ED²
ED² = AD² - AE²
ED² = 13² - 5²
ED² = 169 - 25
ED² = 144
ED = 12
Jadi, ED = FC = 12 cm
Langkah kedua: menghitung luas trapesium.
Luas trapesium = ½ x (jumlah sisi sejajar) x tinggi
Luas trapesium = ½ (AB + DC) x DE
Luas trapesium = ½ (30 + 20) x 12
Luas trapesium = ½ (50) x 12
Luas trapesium = 25 x 12
Luas trapesium = 300 cm²
Jadi luas trapesium adalah 300 cm².
6. Contoh soal keempat dan pembahasannya
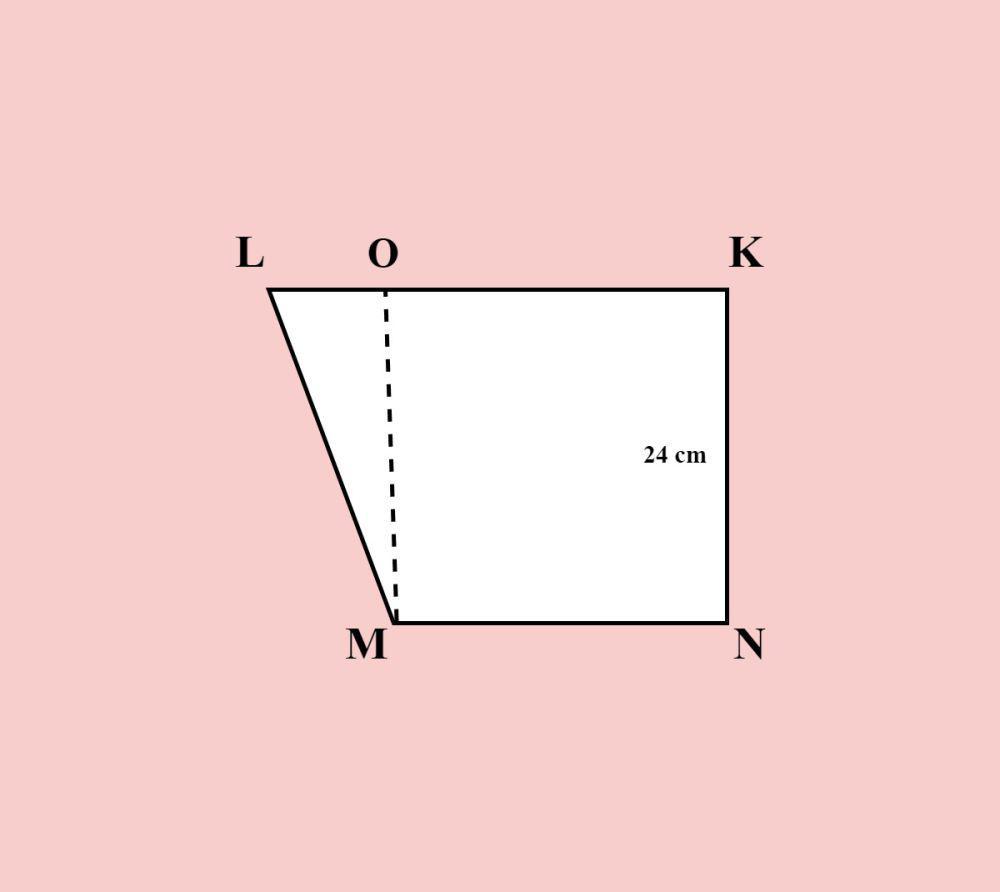
Trapesium KLMN yang berbentuk siku-siku di K, dengan perbandingan panjang sisi KL terhadap MN sebesar 6 : 4, panjang sisi KN adalah 24 cm, dan luas trapesium tersebut adalah 600 cm². Berapa panjang ML?
Pembahasan:
Diketahui:
Trapesium KLMN adalah trapesium siku-siku di K
KL : MN = 6 : 4
KN = 24 cm
Luas trapesium = 600 cm²
KN = OM = 24 cm
KO = NM
OL = KL - MN
Rumus luas trapesium = ½ x (jumlah sisi sejajar) x tinggi = ½ (alas (KL) + atap (MN)) x tinggi
Ditanya:
Panjang ML = ?
Jawaban:
Langkah pertama: mencari panjang KL dan MN.
Karena KL : MN = 6 : 4, kita dapat menyebut panjang KL sebagai 6a dan MN sebagai 4a, di mana a adalah faktor skala.
Jadi:
KL = 6a
MN = 4a
Luas trapesium = 600
Luas trapesium = ½ x (jumlah sisi sejajar) x tinggi
Luas trapesium = ½ (KL + MN) x KN
600 = ½ (6a + 4a) x 24
600 = ½ (10a) x 24
600 x 2 = 10a x 24
1200 = 240a
a = 1200 : 240
a = 5
Maka:
KL = 6a = 6 x 5 = 30 cm
MN = 4a = 4 x 5 = 20 cm
OL = KL - MN = 30 - 20 = 10 cm
Langkah kedua: mencari sisi miring atau kaki2 trapesium.
Karena trapesium KLMN adalah trapesium siku-siku, maka mencari sisi miring dapat menggunakan rumus teorema Pythagoras:
c² = a² + b²
ML² = OL² + KN²
ML² = 10² + 24²
ML² = 100 + 576
ML² = 676
ML = 26
Jadi panjang ML adalah 26 cm.
7. Contoh soal kelima dan pembahasannya
Pada gambar di atas, KLMN adalah trapesium siku-siku di K dengan KL // MN. Panjang KL = 18 cm dan MN = 12 cm. Jika luas trapesium KLMN = 120 cm², maka keliling trapesium KLMN adalah…
Pembahasan:
Diketahui:
KLMN adalah trapesium siku-siku di K
KL = 18 cm
MN = 12 cm
LO = KL - MN = 18 - 12 = 6 cm
Luas trapesium KLMN = 120 cm²
Rumus luas trapesium = ½ x (jumlah sisi sejajar) x tinggi = ½ (alas (AB) + atap (CD)) x tinggi
Tinggi trapesium atau kaki1 => KN = t
Sisi miring trapesium atau kaki2 => ML
Rumus keliling trapesium = alas + atap + kaki1 + kaki2 = KL + MN + KN + ML
Ditanya:
Keliling trapesium KLMN = ?
Jawaban:
Langkah pertama: mencari panjang kaki1 atau tinggi trapesium (KN).
Luas trapesium = ½ x (jumlah sisi sejajar) x tinggi
Luas trapesium = ½ (KL + MN) x tinggi
120 = ½ (18 + 12) x tinggi
120 x 2 = 30 x t
240 = 30t
t = 240 : 30
t = 8
Jadi panjang KN adalah 8 cm
Langkah kedua: mencari panjang kaki2.
Untuk mencari panjang kaki2 yang merupakan sisi miring segitiga siku-siku LOM sekaligus sisi miring trapesium kita dapat menggunakan rumus teorema Pythagoras:
c² = a² + b²
ML² = LO² + OM²
ML² = 6² + 8²
ML² = 36 + 64
ML² = 100
ML = 10
Jadi, ML = 10 cm
Langkah ketiga: menghitung keliling trapesium KLMN.
Keliling trapesium KLMN = alas + atap + kaki1 + kaki2
Keliling trapesium KLMN = KL + MN + KN + ML
Keliling trapesium KLMN = 18 + 12 + 8 + 10
Keliling trapesium KLMN = 48
Jadi keliling trapesium KLMN adalah 48 cm.
Semoga pembahasan ini memberikan wawasan dan memperkuat kemampuan kita dalam menyelesaikan permasalahan terkait trapesium. Jangan lupa untuk terus mengasah kemampuan dan mengeksplorasi lebih banyak konsep matematika. Selamat belajar dan semoga artikel ini memberikan wawasan yang bermanfaat untuk meningkatkan pemahaman matematika kalian!
