Berapakah Jumlah Nol dalam Satu Desiliun?
- Desiliun adalah angka besar setelah triliun, dengan 33 nol di sistem pendek dan 60 nol di sistem panjang.
- Dalam notasi ilmiah, desiliun ditulis sebagai 10^33 dan jarang digunakan dalam kehidupan sehari-hari.
- Awalan "deci-" menunjukkan bahwa desiliun adalah 10^33 (10 pangkat 33) dengan ukuran yang begitu masif.
Pernahkah kamu membayangkan bahwa bilangan besar itu hanya berpatokan pada sebutan juta, miliar, atau bahkan triliun saja? Ternyata, definisi bilangan besar tidak sesempit itu. Siapa sangka jika selain triliun, ada banyak bilangan besar lainnya yang mungkin jarang kita dengar dalam kehidupan sehari-hari. Setelah triliun, kita mengenal kuadriliun, kuintiliun, sekstiliun, septiliun, oktiliun, dan seterusnya. Setiap tingkatan bilangan besar ini memiliki nama dan jumlah nol yang semakin bertambah.
Misalnya, setelah triliun (1 diikuti 12 nol), ada kuadriliun dengan 15 nol, kuintiliun dengan 18 nol, dan angka-angka besar ini terus meningkat dengan pola tertentu. Jika dihitung, bahkan hingga ada istilah lain yaitu desiliun. Namun, apakah benar desiliun ini adalah angka yang nolnya sangat banyak di belakangnya? Kira-kira berapa ya nolnya? Yuk, mari kita cari tahu berapa banyak nol yang ada dalam angka ini dan bagaimana cara menghitungnya.
1. Apa itu desiliun?
Secara definisi, desiliun sendiri merupakan istilah satuan bilangan besar yang umum digunakan dalam penyebutan bilangan angka. Kendati demikian, desiliun bukan satuan bilangan tertinggi karena sebenarnya masih banyak penyebutan lain yang angkanya jauh lebih tinggi dari 1.000 noniliun.
Desiliun adalah angka yang sangat besar yang jarang digunakan dalam perhitungan sehari-hari. Istilah ini sering dijumpai di dalam bidang matematika atau fisika ketika menggambarkan sesuatu yang berukuran sangat besar. Ada perbedaan penulisan desiliun versi Inggris yang perlu diketahui. Dalam bahasa Inggris, istilah “decillion” (desiliun) digunakan untuk angka yang berbeda tergantung pada sistem yang dipakai: sistem pendek (short scale) atau sistem panjang (long scale), melansir Merriem-Webster
- Sistem Pendek (Short Scale): Umum digunakan di Amerika Serikat, Kanada, dan negara-negara lain yang mengadopsi sistem ini. Dalam sistem ini, 1 desiliun berarti 10^33 atau angka 1 yang diikuti oleh 33 nol.
- Sistem Panjang (Long Scale): Lebih umum digunakan di sebagian besar negara Eropa dan negara-negara lain yang mengikuti sistem panjang. Dalam sistem ini, 1 desiliun sebenarnya berarti 10^60 atau angka 1 diikuti oleh 60 nol.
Perbedaan ini bisa menimbulkan kebingungan saat membandingkan angka besar antar bahasa dan budaya, terutama dalam literatur ilmiah atau ekonomi. Di sistem pendek, desiliun lebih cepat mencapai skala angka besar karena kelipatannya berbasis ribuan (10^3), sedangkan di sistem panjang, tiap awalan kelipatan naik sebesar 10^6.
2. Bagaimana cara menentukan jumlah nol pada bilangan desiliun
Di sistem angka internasional atau sistem SI, desiliun adalah angka yang diikuti oleh 33 nol di belakang angka 1. Penulisannya dalam bentuk angka adalah sebagai berikut:
1.000.000.000.000.000.000.000.000.000.000.000.000.000
Desiliun ditulis dengan awalan "deci-", yang artinya 10. Dalam sistem angka besar, awalan ini menunjukkan bahwa desiliun adalah 10^33 (10 pangkat 33). Jadi, desiliun adalah angka 1 diikuti oleh 33 nol.
3. Cara menuliskan bilangan desiliun
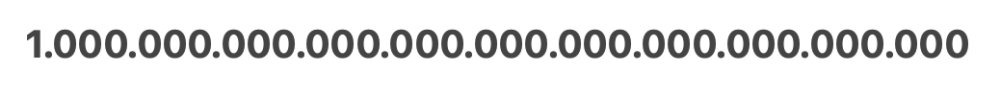
Menulis angka desiliun dapat dilakukan dengan cara berikut untuk memudahkan visualisasi:
1 Desiliun = 1.000.000.000.000.000.000.000.000.000.000.000 (33 nol setelah angka 1)
Dalam notasi ilmiah, angka ini ditulis sebagai 10^33. Nah, gimana? Sekarang kamu jadi tahu kan berapakah jumlah nol pada bilangan desiliun ini? Yap, 33 nol! Angka desiliun ini memang luar biasa besar, dan sangat jarang digunakan dalam kehidupan sehari-hari karena ukurannya yang begitu masif. Angka ini lebih sering muncul dalam perhitungan teoretis di bidang sains, khususnya saat menghitung jumlah partikel atau elemen subatomik di alam semesta.
Jadi, kalau kamu menemukan angka-angka besar seperti ini, kamu sekarang tahu cara mudah untuk memahaminya. Cukup lihat awalan dan jumlah nolnya. Semoga bisa membantu kamu dalam lebih memahami angka-angka besar!
