- 3³ = 3 . 3 . 3
- 4^6 = 6 x 6 x 6 x 6
- (9)^4 = 9 x 9 x 9 x 9
- 2^5 = 5 x 5
Pengertian Eksponen: Sifat, Contoh Soal, dan Pembahasannya

Kalau melihat angka 5972190000000000000000000, bagaimana cara membacanya? Tentu kesulitan, bukan? Maka dari itu, ilmuwan menyederhanakannya menggunakan konsep eksponen. Apa itu?
Well, pada artikel ini, kita akan membahas serba-serbi eksponen. Termasuk pengertian eksponen, sejarah, sifat-sifatnya, hingga contoh soalnya.
Pengertian eksponen
Eksponen merupakan sebuah metode untuk menyatakan bilangan besar dalam bentuk pangkat. Artinya, eksponen mengacu pada sebuah angka dikalikan dirinya sendiri.
Misalnya, 6 x 6 x 6 x 6. Tentu terlalu panjang jika menyebut "enam kali enam enam kali enam...", bukan? Dalam eksponen, pengulangan tersebut cukup disebut 6^4 alias enam pangkat empat.
Contoh lainnya, massa bumi adalah 5972190000000000000000000 kilogram. Nol yang berlebihan ini sulit dibaca, maka secara eksponen menjadi 5.972 x 10^24 kg. Lebih singkat, bukan?
Eksponen disimbolkan dengan pangkat atau tanda (^) yang disebut carrot. Misalnya, empat pangkat dua maka dituliskan 4² atau 4^2.
Sejarah eksponen

Konsep eksponen memang membantu penyebutan nol yang segambreng itu. Namun, dari mana awalnya konsep ini digunakan?
Prosesnya diyakini sudah berlangsung sejak zaman Euclid. Namun, penggunaan eksponen modern diketahui tercatat pertama kali pada buku berjudul Arithemetica Integra.
Buku tersebut ditulis oleh sosok matematikawan Inggris bernama Michael Stifel pada 1544. Sama seperti sekarang, eksponen juga digunakan untuk menyimbolkan pengulangan angka.
Istilah eksponen sendiri berasal gabungan kata dari bahasa Latin, yakni expo yang artinya keluar dan ponere berarti tempat. Secara keseluruhan, eksponen memiliki arti yang berbeda, melansir Sciencing.
Sifat-sifat eksponen
Mirip dengan konsep matematika lainnya, eksponen juga memiliki sifat-sifat khusus. Sifat tersebut nantinya menjadi konsep hitung eksponen.
Sebelumnya, pahami dulu bahwa eksponen terdiri dari 2 komponen. Keduanya adalah ‘basis’ yang merupakan angka di bawah dan ‘pangkat’ yakni angka kecil di atasnya. Misal, 4³ , maka basisnya adalah 4 dan pangkatnya 3.
Adapun sifat-sifat eksponen antara lain:
1. Sifat perkalian
Ketika sebuah perkalian eksponen memiliki basis yang sama dengan pangkat berbeda, kamu tidak perlu repot menghitungnya satu persatu. Tinggal jumlahkan saja pangkatnya. Begini konsepnya:
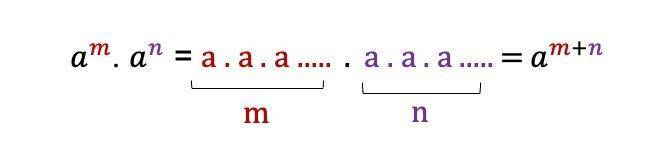
2. Sifat pembagian
Sifat ini berlaku ketika mendapati eksponen pembagian dengan basis sama, tetapi pangkat berbeda. Artinya, kamu bisa mengurangi pangkatnya saja, menjadi:
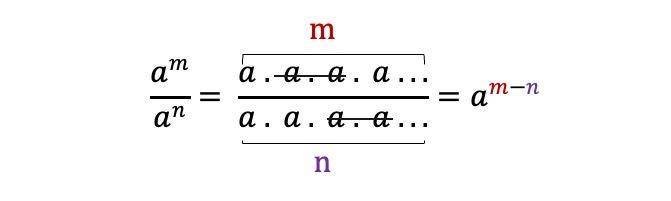
3. Sifat perkalian dengan tanda kurung
Berlaku ketika terdapat dua basis berbeda, tetapi pangkatnya sama. Maka, masing-masing basis bisa dipangkatkan secara terpisah. Ilustrasi konsepnya yakni:
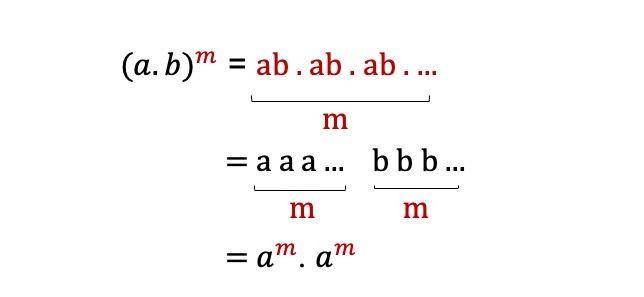
4. Sifat pangkat yang dipangkatkan
Ketika sebuah basis memiliki pangkat, lalu dipangkatkan lagi. Maka, posisi pangkatnya bisa ditukar dan akan memiliki hasil yang sama.
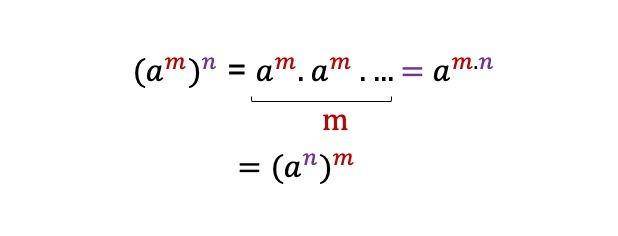
5. Sifat eksponen nol hasilnya satu
Ketika sebuah eksponen memiliki basis dengan pangkat nol, hasilnya adalah 1. Ilustrasinya sebagai berikut:
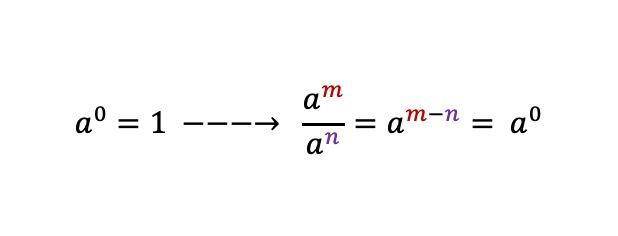
6. Sifat positif diubah menjadi negatif
Sifat ini berlaku ketika eksponen positif berada di posisi penyebut. Kamu bisa mengubahnya dengan basis yang sama menjadi pangkat minus. Ilustrasinya yakni:
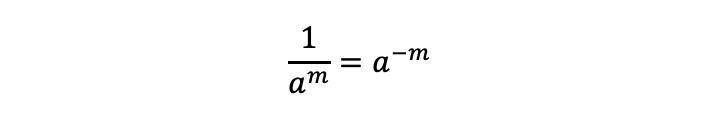
7. Sifat pemangkatan menjadi akar
Kalau kamu menjumpai basis dengan pangkat pecahan, bisa diubah menjadi akar. Misalnya, pada gambar di bawah:
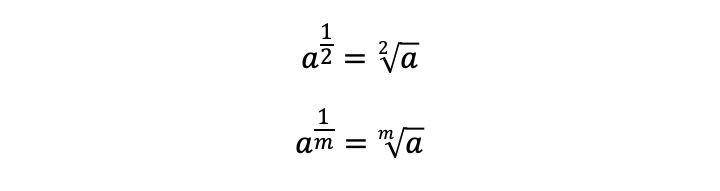
Contoh soal eksponen

Pastikan kamu memahami sifat-sifat eksponen di atas, karena konsep tersebut akan membantu mempermudah proses pengerjaan soal.
Lanjut, saatnya menguji materi melalui praktik soal. Contoh soal dari pengertian eksponen ini bisa jadi lebih sederhana daripada soal ujian dari guru.
Meski demikian, mencoba soal-soal berikut membantu memantapkan pemahaman konsep. Yuk, cus!
Soal 1
Bilangan 6^4 bisa dituliskan sebagai…
a. 6 + 6 + 6 + 6
b. 6 x 6 x 6 x 6
c. 4 x 4 x 4 x 4 x 4 x 4
d. 4 + 4 + 4 + 4 + 4 + 4
Jawaban: B
Catatan: awas terbalik ketika menjabarkan eksponen. Konsepnya adalah basis diulang sebanyak pangkat, bukan sebaliknya, ya.
Soal 2
Manakah pernyataan yang benar dari soal berikut?
a. a dan b
b. a dan c
c. b dan c
d. c dan d
Jawab: B
Soal 3
Sederhanakan (3^2 × 3^-5)/ 9^-2
Catatan: ingat, bahwa simbol (^) menandakan pangkat. Maka:
(3^2 × 3^-5)/ 9^-2
= 3 (^2-5) × 9^2
= 3^-3 × (3^2)^2
= 3^-2 × 34
= 3 (^-2 + 4)
= 3^2
= 9
Oleh karena itu, nilai sederhana dari (3^2 × 3^-5)/ 9^-2 adalah 9.
Pengertian eksponen mudah dipahami, bukan? Konsep ini banyak digunakan di kehidupan sehari-hari, lho! Bisa sebutkan contohnya lagi?