Apa Itu Integral? Ini Jenis, Fungsi, dan Contoh Soalnya
Salah satu materi matematika yang akan kamu jumpai ketika duduk di bangku SMA adalah integral. Ini merupakan cabang ilmu kalkulus yang berkebalikan dengan sifat proses turunan.
Apa itu integral dan bagaimana penyelesaian soalnya? Gulir terus untuk mengetahui materi satu ini.
Apa itu integral?
Dijelaskan sebelumnya bahwa integral merupakan salah satu cabang kalkulus. Sederhananya, integral adalah bentuk penjumlahan bersambung yang bersifat kontinu yang berkebalikan dari turunan
Bersama dengan limit dan turunan, ketiganya saling berkaitan satu sama lain. Contohnya, kalau ada fungsi f(x) diturunkan, maka menjadi f'(x). Ketika dibalik lagi, maka kembali menjadi integral f(x).
Meski saling berkaitan, tidak semua konsep turunan bisa dijadikan integral. Untuk memahaminya, kamu perlu mengetahui rumus dasar integral terlebih dahulu, yakni:
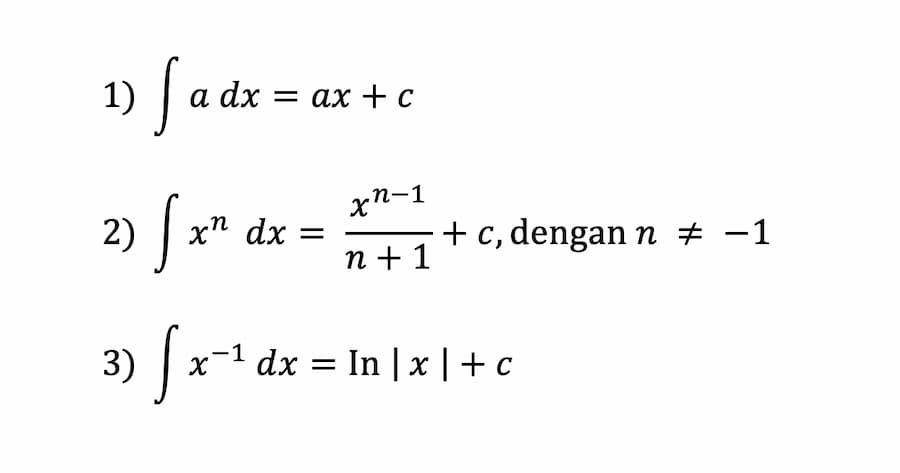
Jenis-jenis integral
Integral terbagi menjadi dua jenis, yakni integral tak tentu dan integral tentu. Keduanya memiliki sifat dan rumus yang berbeda. Apa bedanya?
Integral tak tentu
Integral tak tentu adalah suatu fungsi baru yang memiliki turunan sama seperti fungsi aslinya. Nantinya, hasil dari penghitungan berupa fungsi dalam variabel tertentu dan masih memuat konstanta integrasi.
Jenis integral ini tidak punya batas dan nilai yang jelas. Oleh sebab itu, seringkali nilainya dilambangkan dengan konstanta C. Di samping itu, integral tak tentu memiliki batas atas ataupun bawah karena bersifat unlimited. Rumus integral tak tentu yakni:
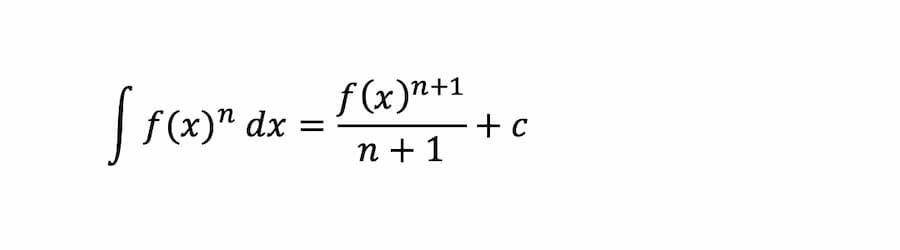
Sifat integral tak tentu
Integral tak tentu memiliki sifat yang menjadikannya khas. Berikut adalah sifat dari integral tak tentu.
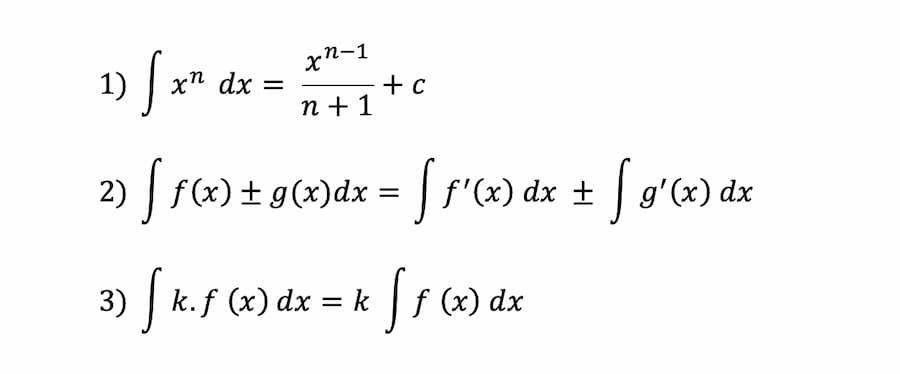
Penerapan integral tak tentu
Rumus-rumus integral tak tentu dipakai buat apa, sih? Bukan hanya pada matematika tekstual, penghitungan ini digunakan dalam bidang fisika. Misalnya, ketika mencari jarak, kecepatan, dan/atau percepatan.
Integral tentu
Beda dengan jenis sebelumnya, integral tentu memberikanmu kepastian. Artinya, integral ini sudah punya nilai awal dan akhir. Terdapat batasan yang jelas pada batas atas dan batas bawah.
Kamu bisa mengidentifikasi integral tentu dengan adanya keterangan 'ab' pada lambang integral. 'a' berarti batas bawah dan 'b' merupakan batas atas variabel integral.
Sifat integral tentu
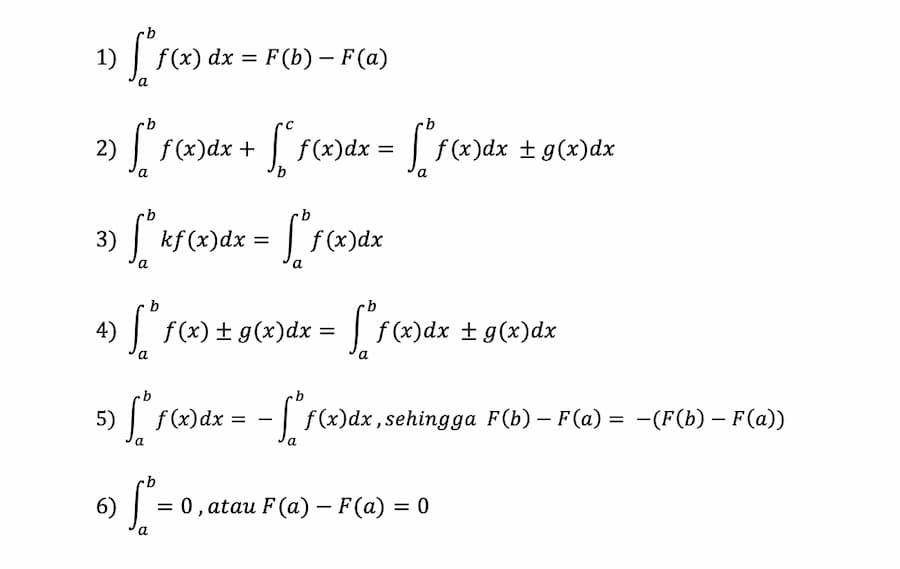
Penerapan integral tentu
Sama seperti versi tidak tentu, integral tentu digunakan untuk kehidupan sehari-hari. Biasanya dipakai untuk mencari dan menghitung luas daerah yang tidak beraturan dan volume benda putar.
Teknik Integral
Apa sudah selesai pembahasannya? Belum, dong. Masih ada teknik integral, yakni cara untuk menyelesaikan persamaan integral itu sendiri. Ada banyak teknik integral, tetapi yang paling sering muncul adalah substitusi dan parsial.
1. Teknik integral substitusi
Teknik integral substitusi digunakan ketika sedang menghadapi soal yang kompleks. Nantinya, integral disederhanakan dan kamu bisa memilih salah satu fungsi yang dapat diturunkan. Sisanya, kamu tinggal menghitung dengan substitusi.
Rumus integral substitusi dan contohnya:

2. Teknik integral parsial
Menggunakan teknik integral parsial berarti memisahkan dua fungsi berbeda. Meski demikian, keduanya memiliki variabel yang sama. Rumusnya, yakni:
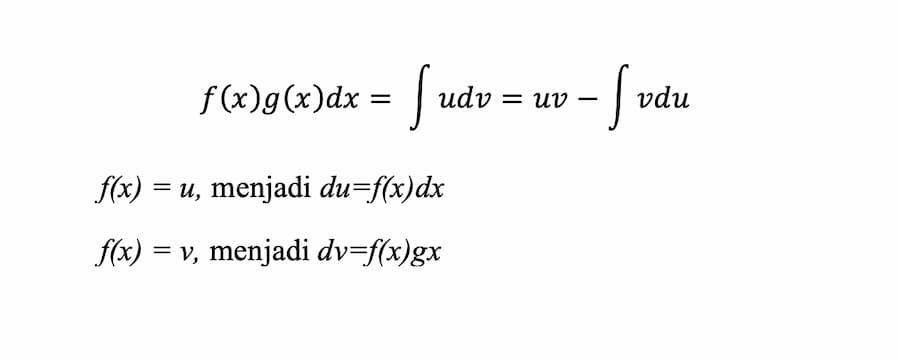
Ketentuan lainnya yakni f(x) punya derajat n yang lebih besar dari 1 dan n merupakan bilangan asli. Agar lebih mudah, coba turunkan f(x) dan integralkan g(x) seperti pada tabel berikut.
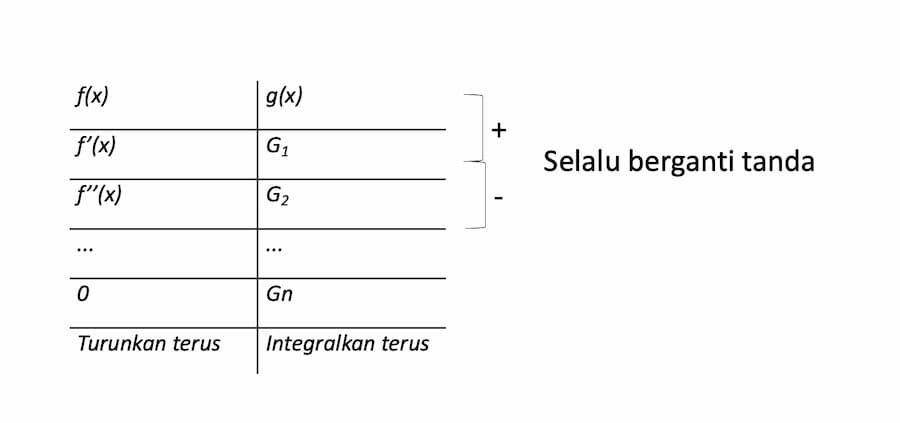
Cara menghitung dengan tabel di atas yakni menerapkan perkalian silang f(x) dengan G1, lalu kali silang juga turunan f'(x) dengan G2, dan seterusnya. Hasil penghitungan nanti berganti positif dan negatif berurutan.
Adapun penghitungan tabel di atas dapat menjadi rumus sederhana berikut:
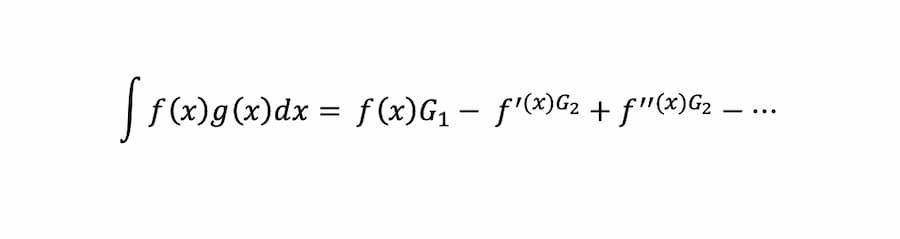
Sudah mumet dengan materi integral ini? Coba pahami secara perlahan, ya. Materi ini sebenarnya cukup menantang untuk diselesaikan.