Rumus Aljabar: Bentuk, Operasi, dan Contoh Perhitungannya

Menurut buku Bentuk Aljabar karya Noor Hidayani, bentuk aljabar merupakan bentuk yang memuat angka dan variabel (simbol) yang digunakan untuk merepresentasikan bilangan secara umum atau untuk menyederhanakan suatu bilangan. Misalnya, x mewakili bilangan yang diketahui, y untuk mewakili bilangan yang ingin diketahui.

Selain x dan y, lambang atau simbol yang dapat digunakan untuk menyatakan variabel adalah huruf kecil, seperti a, b, c, p, q, r, z, dan lain sebagainya. Agar lebih mudah dalam memahami rumus aljabar, berikut adalah bentuk-bentuknya.

Suku merupakan bentuk aljabar berupa variabel atau konstanta yang dipisahkan oleh tanda operasi penjumlahan (+) atau pengurangan (-). Dalam mempelajari rumus aljabar, bentuk aljabar dibagi menjadi suku satu, suku dua, suku banyak, dan suku sejenis. 

1. Suku satu atau suku tunggal, yakni bentuk aljabar yang terdiri atas satu suku.
2. Suku dua (binomial), yakni bentuk aljabar yang terdiri atas dua suku.
3. Suku banyak (polynomial), terdiri atas lebih atau sama dengan dua suku.
4. Suku sejenis, yaitu suku-suku dengan variabel dan pangkat yang sama.

Contoh:

Suku satu: x, 2b, -5p, 3, 4y²

Suku dua:

3 + a (3 merupakan suku pertama, dan a merupakan suku kedua).

x² + 2x (x² merupakan suku pertama, dan 2x merupakan suku kedua).

Suku banyak:

x² + 2x - 5 (x² adalah suku pertama, 2x suku kedua, dan -5 suku ketiga)

a + b - 2c + 1 (a merupakan suku pertama, b suku kedua, -2c suku ketiga, dan 1 suku keempat).

Suku sejenis:

x dan -5x (sejenis, karena sama-sama memiliki variabel x)

3y² dan 2y² (sejenis, karena sama-sama memiliki variabel y²)

Faktor merupakan bilangan yang membagi bilangan lain, atau hasil perkalian. Misalnya:

Bentuk aljabar x × y × z atau xyz memiliki faktor x, y, dan z.

Konstanta adalah lambang aljabar yang menunjukkan anggota tertentu (berupa bilangan) dalam himpunan semestanya. 

Koefisien adalah bagian konstanta dari suku aljabar yang menunjukkan banyaknya variabel atau simbol. Misalnya suku -2ab, maka -2 merupakan koefisien dari variabel ab. 

Agar lebih memahami mengenai rumus aljabar berdasarkan bentuknya, berikut adalah contohnya:

1. Bentuk aljabar 3x + 5

Variabel: x

Koefisien dari x adalah 3

Konstanta: 5 

2. Pada bentuk aljabar 2x + 8xy

Variabel: x dan y

Koefisien dari x: 2

Koefisien dari xy: 8

Tidak ada konstanta dalam bentuk aljabar tersebut.

Sama seperti operasi penghitungan dalam bilangan bulat, rumus aljabar juga menggunakan operasi hitung berupa penjumlahan, pengurangan, perkalian, dan pembagian. Berikut ini penjelasannya.

Penjumlahan

Perlu diketahui, dalam bentuk aljabar, operasi penjumlahan hanya dapat dikerjakan pada suku-suku yang sejenis. Untuk itu, jika ada suku-suku yang berbeda atau tidak sejenis, maka bilangannya tidak dapat dijumlahkan (ditulis sebagai tetap). Misalnya:

3x + 2y = 3x + 2y (Tetap)

Sementara itu, pada bentuk aljabar 5a + a + 2a dapat dijumlahkan, dengan hasilnya sebagai berikut:

5a + a + 2a = (5 + 1 + 2)a = 8a

Contoh lainnya, tentukan hasil penjumlahan dari bentuk suku aljabar berikut: a + 2b + 4b +3a.

Jawab:

a + 2b + 4b +3a = a + 3a + 2b + 4b (kumpulkan suku sejenis)

= (1 + 3)a + (2 + 4)b 

= 4a + 6b.

Pengurangan

Dalam menggunakan rumus aljabar, operasi pengurangan pada bentuk aljabar juga sama seperti penjumlahan, yakni hanya bisa dikerjakan pada suku-suku yang sejenis. Untuk lebih jelasnya, simak beberapa contoh berikut.

1. 5x - 2y = 5x - 2y (Tetap)

2. 4m - 15m = (4 - 15)m = -11m

24p - 3 - 15p - 5 

= 24p - 15p - 3 - 5  (kelompokkan suku-suku sejenis)

= (24 - 15)p - 3 - 5

= 9p - 8

Pada dasarnya, operasi perkalian dalam bentuk rumus aljabar merupakan perkalian antara koefisien dengan koefisien, dan variabel dengan variabel. Namun, dalam bentuk aljabar operasi perkalian dibedakan menjadi perkalian antar-variabel sejenis dan antar-variabel tidak sejenis. Berikut contohnya:

1.  2 × a = 2a

2. a × b = ab

3. 2a × 3b = 2 × 3 × a × b = 6ab

4. a × a = a²

5. 2a² × 5ab = 2 × 5 × a² × ab = 10a³b

6. a² × a3 = a²+³ = a⁵

7. (ax + b) (cx + d) 

= (ax + cx + ax × d) + (b × cx + b × d)

= acx2 + (ad + bc )x + bd

Bentuk operasi pembagian dalam rumus aljabar antar-variabel sejenis akan menghasilkan variabel dengan pangkatnya berupa hasil pengurangan dari pangkat variabel tersebut. Misalnya: 2x : x (pembagian suku sejenis)

x² : x (pembagian suku tidak sejenis)

Setelah mengetahui apa saja bentuk dan operasi rumus aljabar, sekarang kamu sudah mengerti bagaimana cara membedakannya, bukan? Nah, agar kamu bisa memahami lebih mendalam mengenai rumus aljabar, berikut adalah beberapa contoh soalnya yang bisa kamu ikuti, seperti:

1. Sederhanakan bentuk aljabar berikut ini!

(26x² - 6x + 14) + (32x² +4x - 56)

= 26x² - 6x +14 +32x² + 4x - 56

= 26x² +32x² - 6x + 4x - 56 (kelompokkan suku sejenis)

= (26 +32)x² + (-6 + 4)x + (14 - 56)

= 58x² - 2x - 42

2. (4ab + 3a -5) - (ab -a + 3)

= 4ab + 3a -5 - ab - (-a) - 3

= 4ab + 3a -5 - ab + a - 3

= 4ab - ab + 3a + a -5 - 3 (kelompokkan suku sejenis)

= (4 - 1)ab + (3 + 1)a - 8

= 3ab + 4a - 8

3. (2x - 1) (5 - 3x)

= 2x (5 - 3x) - 1(5 - 3x)

= 2x × 5 - 2x × 3x - 1 × 5 - 1 × (-3x)

= 10x - 6x² - 5 + 3x

= -6x² + 3x + 10x - 5 (kelompokkan suku sejenis)

= -6x² + 13x - 5

4. Tentukan hasil pembagian pecahan aljabar berikut ini!

Soal rumus aljabar

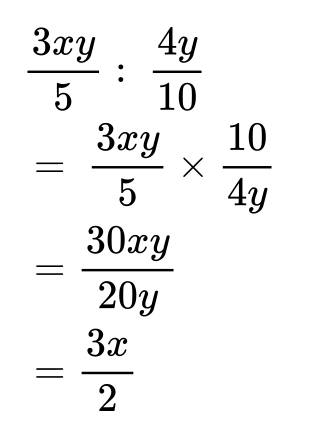
Demikian penjelasan mengenai rumus aljabar, mulai dari bentuk-bentuknya, operasi penjumlahan dan pengurangan, perkalian dan pembagian, hingga contoh soal serta pembahasannya. Semoga dengan informasi di atas dapat membantumu dalam mempelajari rumus aljabar lebih dalam lagi, ya.

Penulis: Muti'ah Nur Rahmah