Transpose Matriks: Pengertian dan Contoh Soalnya
Di antara jenis-jenis operasi hitung matriks, ada yang namanya materi transpose matriks. Cabang ilmu matematika ini mempelajari pertukaran posisi matriks. Adapun matriks sendiri merupakan susunan bilangan dalam baris dan kolom yang disebut elemen.
Bagaimana cara menghitung transpose matriks? Yuk, simak uraian materi sekaligus contoh soal dan pembahasannya di bawah ini!
Pengertian transpose matriks
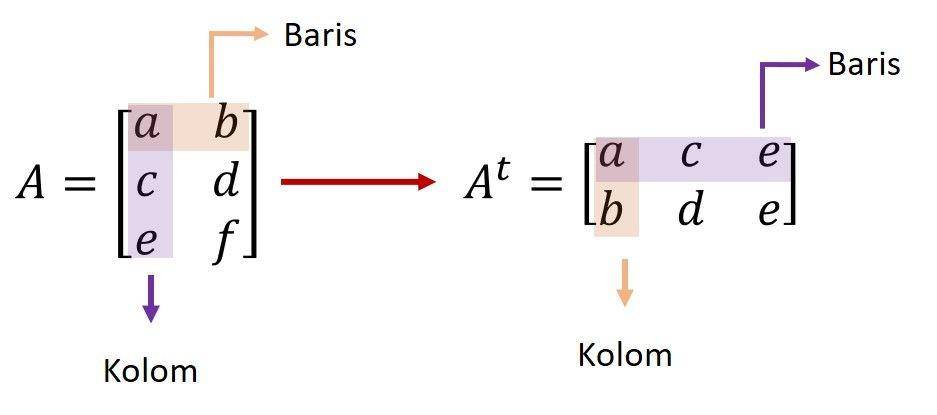
Transpose matriks adalah operasi mengubah baris matriks menjadi kolom dan kolom menjadi baris. Lebih jelasnya, lihat pada gambar.
Hasil dari pertukaran ini dikonotasikan dengan petik atas. Misalnya, matriks A, maka transpose matriksnya adalah A’ atau At.
Konsepnya, jika matriks A berukuran mxn, maka transpose matriks A berukuran nxm. Operasi hitung transpose hanya berlaku untuk matriks dan vektor, karena skalar hanya memiliki satu baris dan kolom.
Jika dari operasi transpose menghasilkan bentuk matriks awal, disebut sebagai matriks simetris. Artinya, A = A’.
Transpose matriks juga memiliki sifat-sifat tertentu yang membantu operasi hitung, yakni:
(AT)T = A
(A + B)T = AT + BT
(A – B)T = AT – BT
(kA)T = k.AT dengan k adalah konstanta
(AB)T = BTAT
Contoh soal transpose matriks
Nah, agar makin mantap memahami konsep transpose matriks, coba kerjakan latihan soal di bawah ini. Soal-soal berikut merupakan hitungan dasar yang mengubah baris menjadi kolom dan kolom menjadi baris.
Tipsnya, perhatikan dengan benar urutan elemen dan letaknya. Biar gak bingung, kamu bisa menandai terlebih dahulu dan gak keliru meletakkan angka.
Soal Transpose Matriks 1
Diketahui bentuk matriks transpose sebagaimana pada gambar. Tentukan bentuk matriksnya.
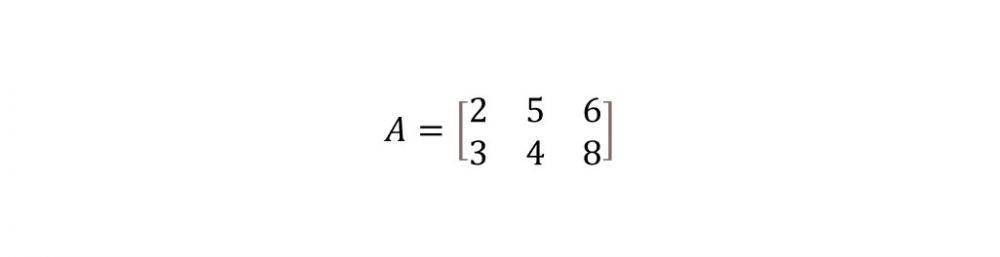
Catatan: meski diketahui bentuk transpose matriks, cara mengubah ke matriks tetap sama yakni meletakkan elemen baris ke kolom dan kolom ke baris.
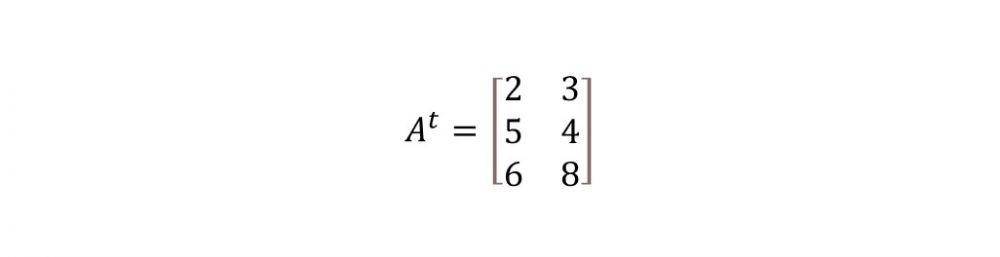
Soal Transpose Matriks 2
Carilah transpose matriks dari bentuk matriks berikut ini!
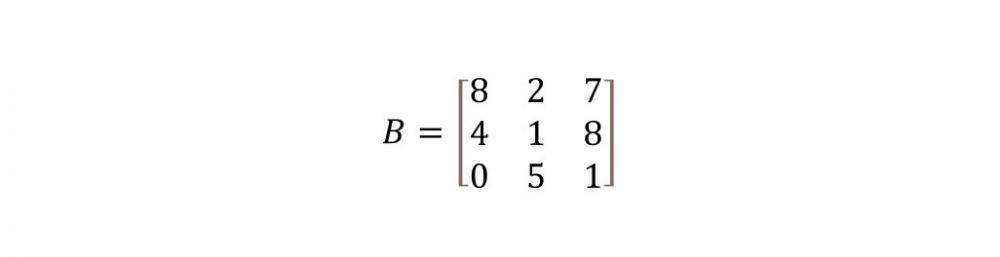
Pembahasan:
Matriks B memiliki elemen dengan susunan:
- baris pertama: 8, 2, dan 7
- baris kedua: 4, 1, dan 8
- baris ketiga: 0, 5, dan 1
- kolom pertama: 8, 4, dan 0
- kolom kedua: 2, 1, dan 5
- kolom ketiga: 7, 8, dan 1
Maka, susunan matriks transpose B adalah:
- baris pertama: 8, 4, dan 0
- baris kedua: 2, 1, dan 5
- baris ketiga: 7, 8, dan 1
- kolom pertama: 8, 2, dan 7
- kolom kedua: 4, 1, dan 8
- kolom ketiga: 0, 5, dan 1.
Soal Transpose Matriks 3
Ada dua buah matriks seperti pada gambar
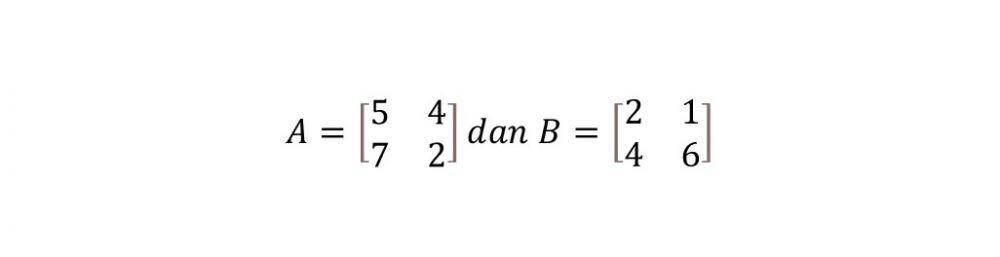
Tentukan besar (A+B)t!
Kalau menemukan soal seperti ini, kamu perlu menghitung A+B terlebih dahulu sebelum ditranspose.
Gimana, operasi hitung transpose matriks cukup sederhana, bukan? Memahami materi ini akan membantu kamu melanjutkan ke pelajaran matematika yang lebih kompleks.
