“Pada segitiga siku siku berlaku bahwa kuadrat hipotenusa sama dengan jumlah kuadrat dari dua sisi yang lainnya.”
Rumus Pythagoras, Sejarahnya, dan Contoh Soal Pythagoras

Saat bertemu bangun segitiga dengan salah satu sisi yang gak diketahui, Pythagoras adalah koentji. Namun, ada syarat-syarat tertentu agar rumus ini bisa digunakan.
Rumus ini mungkin terdengar gak asing, sebab telah diperkenalkan bertahap sejak duduk di bangku sekolah dasar. Gulir sampai bawah, untuk belajar sama-sama rumus pythagoras dan contoh soal Pythagoras.
Apa itu rumus Pythagoras?

Teorema Pythagoras pertama kali tercatat di masa Babel dan Mesir Kuno. Masa itu dimulai sekitar 1.900 SM. Asumsi ini didasarkan pada tulisan yang termuat pada tablet Babilonia berusia 4.000 tahun yang bernama Plimpton 322, melansir situs Universitas California.
Selain itu, penghitungan segitiga dengan panjang sisi 3, 4, dan 5 satuan panjang yang membentuk segitiga siku siku juga tercatat di sejarah lain. Salah satunya dalam Baudhayana Sulbasutra India. Bukti ini ditulis antara 800 dan 400 SM yang menyebutkan triple Pythagoras.
Namun, penggunaan cara hitung tersebut gak terkonsep hingga masa Yunani Kuno. Seorang filsuf dan ilmuwan bernama Pythagoras, mencetuskan teori yang akhirnya merujuk pada namanya, teorema Pythagoras. Sosok Pythagoras sendiri hidup di Pulau Samos, di Laut Aegea, masa 570-495 SM atau sekitar abad ke-6 sebelum Masehi.
Rumus Pythagoras
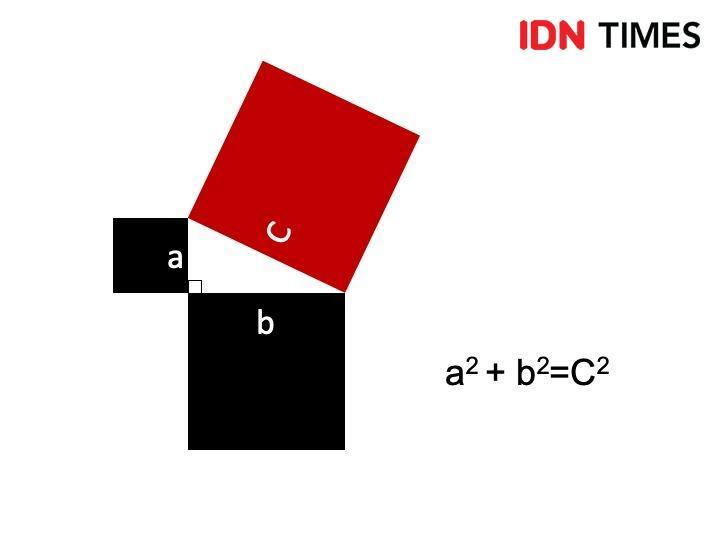
Pythagoras menyebutkan bahwa segitiga siku-siku atau segitiga yang memiliki sudut 90 derajat kuadrat sisi miringnya sama dengan jumlah kuadrat sisi lainnya. Berlaku juga pada penghitungan luas segitiga. Atau, jika dituliskan rumus pythagoras menjadi seperti pada gambar.
Adapun bunyi teorema Pythagoras sendiri yakni:
Pembuktian teorema Pythagoras bisa dilakukan dengan melihat gambar di atas. Persegi yang terbentuk dengan menarik garis dari masing-masing segitiga, jika dihubungkan menggunakan rumus a2 + b2 = c2 berarti persegi a+b sama luasnya dengan persegi c.
Rumus Pythagoras

Kalem dulu, penjelasan di atas merupakan cikal bakal dan breakdown dari konsep teorema Pythagoras. Dari pengertian di atas, maka rumusnya bisa dijabarkan menjadi:
- c2 = a2 + b2 atau c = √a2 + b2
- a2 = c2 – b2 atau a = √c2 – b2
- b2 = c2 – a2 atau b = √c2 – a2
Rumus Pythagoras di atas, bisa kamu gunakan untuk mengetahui sisi segitiga siku-siku. Tinggal masuk-masukkan angkanya saja. Namun, ada beberapa trik yang bisa kamu pahami dan hafal untuk hitung cepat.
- 3, 4, 5
- 5, 12, 13
- 6, 8, 10
- 7, 24, 25
- 8, 15, 17
- 9, 12, 15
- 10, 24, 26
- 12, 16, 20
- 14, 48, 50, dan seterusnya.
Nah, maksud tiga angka di atas adalah kalau kamu punya segitiga dengan dua sisi memiliki panjang 3 dan 4, maka bisa diketahui panjang satu sisi yang belum diketahui adalah 5. Begitu pula seterusnya. Dengan panduan ini, kamu bisa mencari tahu dan menghitung rumus Pythagoras.
Rumus Pythagoras dan contoh soal Pythagoras
Biar makin memahami konsepnya, langsung kerjakan contoh soalnya saja, yuk! Penerapan rumus Pythagoras dan contohnya berikut lebih sederhana dari soal ujian. Semoga bisa mudah dipahami, ya!
Contoh soal Pythagoras 1
Sebuah segitiga siku siku ABC memiliki tinggi BC 5 cm dan alas AC 12 cm. Berapa sisi miring AB?
Pembahasan:
AB2 = BC2 + AC2
AB2 = 52 + 122 (2 di sini merupakan kuadrat)
AB2 = 25 + 144 = 169
AB = √169 = 13
Jadi, sisi miring AB adalah 13 cm.
Coba bandingkan dengan list triple Pythagoras di atas. Benar bukan? Kalau kamu menghafal kombinasi angka-angka tersebut, maka bisa lebih cepat mengerjakan soal Pythagoras.
Contoh soal Pythagoras 2
Lanjut, perhatikan gambar di atas. Kira-kira, berapa nilai a atau panjang sisi tegak dari segitiga siku-siku tersebut?
Pembahasan:
Karena dicari a, maka:
a2 = c2 – b2
a2 = 502 – 142
a2 = 2.500 – 196
a2 = 2.304
a = √2.304
a = 48 cm.
Jadi, panjang sisi a dari segitiga siku-siku pada gambar adalah 48 cm.
Catatan, jangan lupa menambahkan satuan panjang sesuai dengan yang diminta pada soal, ya. Kecuali jika memang gak dicantumkan, maka kamu wajib memberikan satuan panjangnya (cm, m, dan sebagainya).
Contoh soal Pythagoras 3
Pak Jungkook melihat sebuah segitiga ABC dengan siku-siku di titik B. Karena gabut, Pak Jungkook ingin tahu berapa panjang sisi miring segitiga tersebut jika diketahui panjang AB = 16 cm dan BC = 30 cm ?
Pembahasan:
AC2 = AB2 + BC2
AC2 = 162 + 302 (2 di sini merupakan kuadrat)
AC2 = 256 + 900
AC2 = 1156
AC = √1156
AC = 34 cm
Tanda tanya Pak Jungkook terjawab bahwa sisi miring segitiga tersebut memiliki panjang 34 cm.
Teorema rumus Pythagoras dan contoh Pythagoras di atas mudah dipahami, bukan? Selanjutnya, kamu bisa menerapkan rumus ini pada kehidupan sehari-hari jika dibutuhkan.