- a^m x a^n = a^(m + n)
- a^m ÷ a^n = a^(m-n)
- (a^m)^n = a^mn
- (ab)^m = a^m b^m
- (a/b)^m = a^m/b^m
- a^0 = 1
- a^(-m) = 1/a^m
7 Sifat Eksponen yang Harus Kamu Ketahui
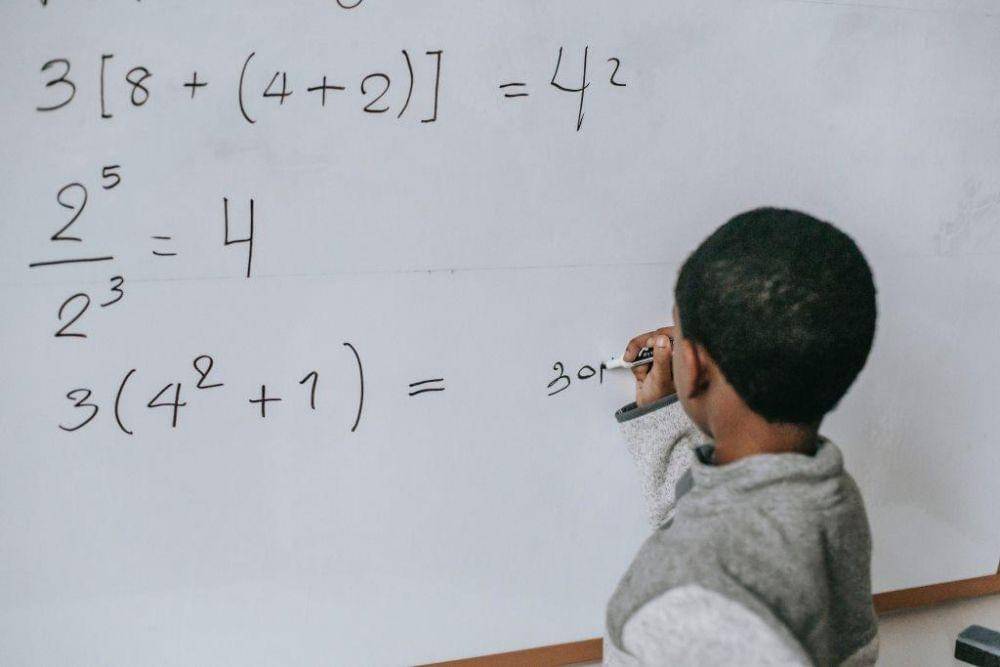
Kita sering membaca angka dalam satuan bilangan seperti puluhan, ratusan, ribuan, jutaan, dan lain sebagainya. Lalu, angka apa yang memiliki digit lebih banyak daripada yang bisa kita baca?
Misalnya, massa bumi adalah 5972190000000000000000000 kg. Angka tersebut tidak bisa dibaca dengan kata-kata sederhana. Sehingga untuk mengucapkan jenis angka itu kita harus menggunakan eksponen. Yakni menjadi 5.972 x 10^24 kg.
Nah, mengenai apa itu eksponen dan bagaimana sifat-sifat eksponen tersebut, kita cari tahu selengkapnya lewat artikel ini.
Pengertian eksponen
Melansir situs Byju's, eksponen adaah metode untuk menyatakan bilangan besar dalam bentuk pangkat. Hal itu berarti bahwa eksponen mengacu pada berapa kali angka dikalikan dengan dirinya sendiri.
Misalnya, 5 dikalikan dengan dirinya sendiri sebanyak 4 kali, yaitu 5 x 5 x 5 x 5. Itu dapat ditulis sebagai 5⁴ . Di sini 5 adalah bilangan basis, dan pangkat empat (⁴ ) adalah eksponen. Angka tersebut dapat dibaca menjadi 5 pangkat 4. Tanpa eksponen, suatu bilangan yang dioperasikan berulang akan sulit ditulis. Karena lebih mudah menulis 5⁴ daripada menulis 5 x 5 x 5 x 5.
Simbol yang digunakan untuk mewakili eksponen adalah tanda ^. Misalnya, 4 dipangkatkan dua bisa ditulis menjadi 4^2 atau 4² .
Sifat-sifat eksponen
Sifat-sifat eksponen, juga dikenal sebagai sifat-sifat bilangan berpangkat, adalah aturan-aturan yang mengatur bagaimana operasi matematika seperti perkalian, pembagian, dan perpangkatan bekerja pada bilangan berpangkat. Merujuk laman Cuemath, sifat-sifat eksponen adalah seperti aturan utama eksponen yang harus diikuti saat menyelesaikan eksponen.
Sifat-sifat eksponen yang berbeda dijelaskan berdasarkan kekuatan yang dimiliki. Pada dasarnya terdapat dua hukum eksponen, yakni hukum perkalian dan hukum pembagian. Dari situ, akan dibagi lagi menjadi tujuh sifat-sifat eksponen berikut ini:
Sifat-sifat tersebut digunakan untuk menyederhanakan ekpsresi aljabar yang kompleks dan menulis bilangan besar dengan cara yang dapat dimengerti. Masing-masing sifat eksponen akan dijelaskan melalui poin berikutnya.
Sifat eksponen perkalian (law of product)
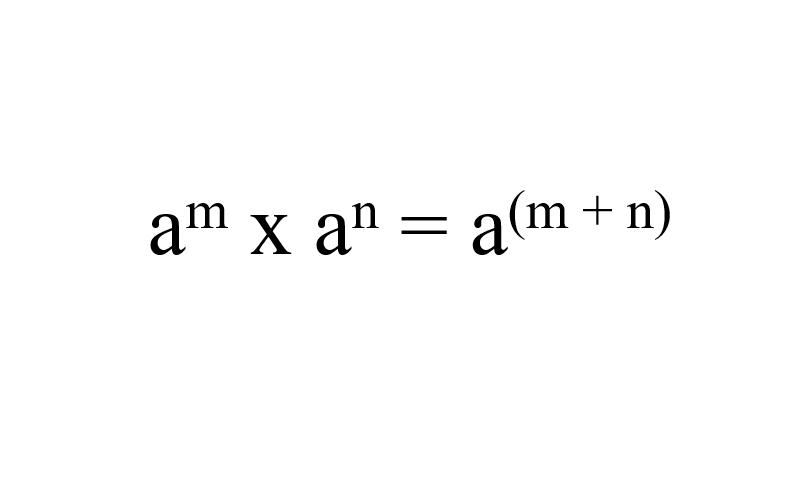
Sifat eksponen pertama terkait dengan aturan perkalian. Di mana law of product menyatakan bahwa aturan dari dua bilangan atau lebih dengan basis yang sama, nilainya sama dengan basis umum pangkat dari jumlah eksponen.
Hal itu berarti jika kita mengkalikan angka basis yang sama, meski dengan eksponen yang berbeda, maka kita hanya perlu menjumlahkan eksponen tersebut.
Contoh:
2² x 2⁴ = 2 (² + ⁴)
= 2⁶
= 64
Sifat eksponen pembagian (law of quotient)
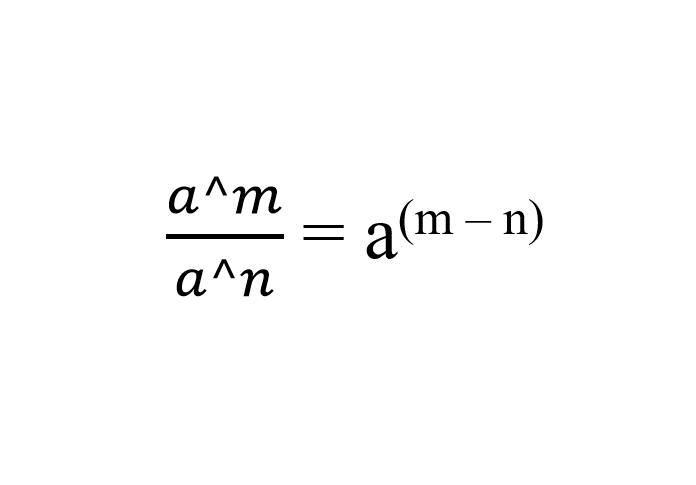
Sifat pembagian eksponen menyatakan bahwa hasil bagi dari dua bilangan atau lebih dengan angka basis yang sama, bernilai sama dengan basis umum pangkat dari selisih eksponen. Artinya, jika kita membagi angka basis yang sama, meski dengan eksponen yang berbeda, maka kita hanya perlu melakukan operasi pengurangan pada eksponen tersebut.
Contoh:
2⁴ ÷ 2² = 2 (⁴ - ² )
= 2²
= 4
Sifat eksponen pangkat dari pangkat (law of power of power)
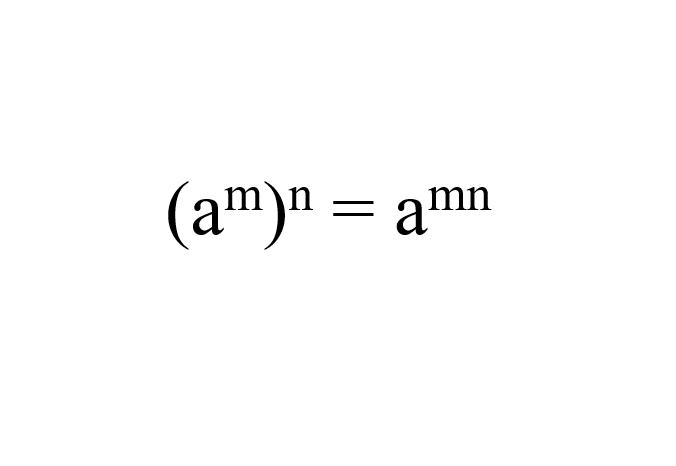
Sifat eksponen ketiga berhubungan dengan pangkat dari eksponen. Di mana ketika ingin mencari tahu pangkat dari bilangan yang dipangkatkan menjadi eksponen, kita hanya perlu mengalikan eksponen-eksponen tersebut.
Misalnya:
(2⁴)² = 2(⁴x²)
= 2⁸
= 256
Sifat eksponen pangkat dari hasil kali (law of power of a product)
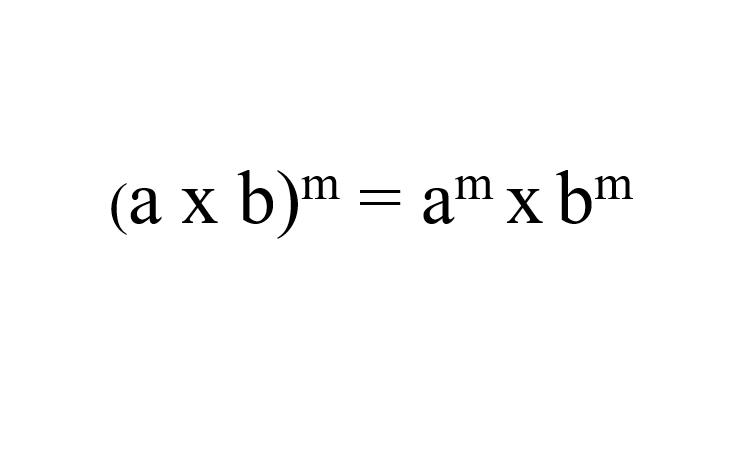
Selanjutnya kita memasuki sifat eksponen keempat. Di mana ketika dua angka basis dipangkatkan dengan eksponen yang sama, maka akan ditemukan jawaban yang setara seperti saat masing-masing angka dikalikan dengan eksponen secara terpisah.
Dengan kata lain, hasil kali dari dua bilangan berbeda dengan eksponen yang sama adalah bernilai sama dengan perkalian dari setiap bilangan dengan eksponen tersebut.
Misal:
(2 x 3)² = 2² x 3²
= 4 x 9
= 36
Sifat eksponen pangkat dari hasil bagi (law of power of a quotient)
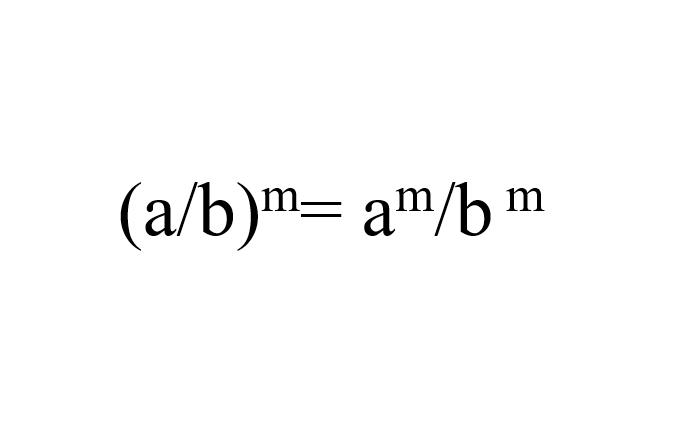
Sifat eksponen power of a quotient menyatakan bahwa pembagian dari dua angka yang dipangkatkan akan memunculkan jawaban yang sama, dengan hasil pembagian dari setiap angka yang memiliki eksponen secara terpisah.
Hal itu berarti bahwa saat kita menaikkan hasil bagi menjadi pangkat, kita menaikkan pembilang dan penyebutnya menjadi pangkat.
Contoh:
(4/2)² = 4/2 x 4/2
= 4 x 4/2x 2
= 4²/2²
= 16/4
= 4
Sifat eksponen pangkat nol (law of a zero exponent)
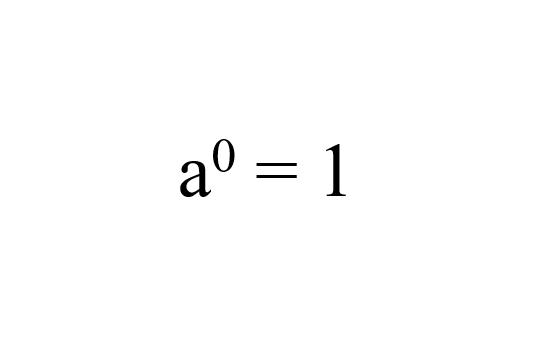
Nah, sifat eksponen pangkat nol ini sangat sederhana. Law of a zero exponent menyatakan bahwa bilangan berapa pun yang dipangkatkan dengan nol (0) maka nilainya adalah satu (1).
Hal itu menurut Math Planet didapatkan dari contoh persamaan berikut:
1 = a²/a²
= a²-²
= a⁰
a⁰ = 1
Sifat eksponen berpangkat negatif (law of negative exponent)
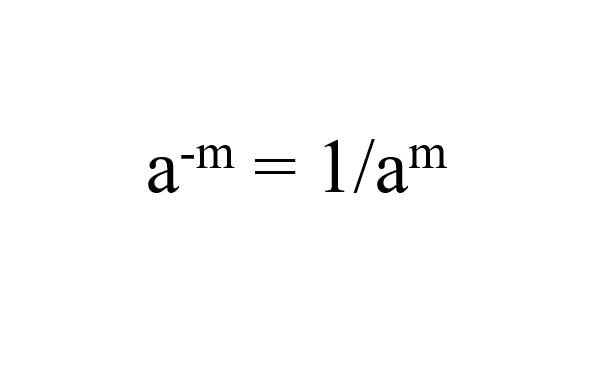
Memasuki sifat eksponen yang ketujuh, sifat ini berhubungan angka basis yang memiliki eksponen negatif. Di mana aturan eksponen negatif menyatakan bahwa basis dengan eksponen negatif adalah sama dengan kebalikan dari basis yang dinaikkan menjadi kebalikan dari eksponen.
Eksponen negatif memberi tahu berapa kali kita harus mengalikan dari basis. Misalnya, jika diberikan a^(-m), maka dapat diekspansi menjadi 1/a^m, sesuai ilustrasi di atas. Hal ini berarti bahwa kita harus mengalikan kebalikan dari a, yaitu 1/a sebanyak pangkat 'm' kali.
Eksponen negatif digunakan saat menulis pecahan dengan eksponen. Beberapa contoh eksponen negatif yang diubah menjadi eksponen positif adalah:
- 2 x 3-⁹ = 2 x (1/3⁹) = 2/3⁹
- 7-³ = 1/7³
- 67-5 = 1/67⁵
Ketujuh sifat-sifat eksponen yang telah dijabarkan tersebut adalah aturan dasar dari operasi bilangan berpangkat. Dengan mengetahui sifat eksponen, kini kamu jadi lebih paham harus dengan cara apa menyelesaikan tiap soal bilangan berpangkat, kan?
Penulis: Dian Rahma Fika Alnina














































